各種プロセスシミュレーターには各種物性値が内蔵されていますが、自作物性推算ツールの精度確認や、どの物性推算法を用いるのが良いかを確認する場合、しばしば他のDBとの比較が有益となる場合があります。以下、いくつか無料でアクセスが可能な物性のデータベースをご紹介します。

DIPPR

DIPPR(Design Institute for Physical Property Data)へのリンクはこちらになります。

アカウントを作成するだけで、物性を調べることが可能です。

以下例えばMethaneの物性を調べる場合です。（valueは転載するわけにいかないので、塗りつぶしていますが、実際に検索していただくと値を確認することが可能です）

NIST Chemistry WebBook

NIST(National Institute of Standards and Technology) web bookへのリンクはこちらです。

アカウントの作成も不要で物性の検索ができます。以下は例えば検索画面からMethaneの物性を調べる場合です。どういった物性値を調べたいかのチェックを忘れないようにしてください。（物性値については転載するわけにいかないので、塗りつぶしていますが、実際に検索していただくと値を確認することが可能です）

またREFPROPを購入されている方は、ExcelやPython等からの物性呼び出しが可能です。

自作の物性ツールの精度確認や、プロセスシミュレーターの中で、どの物性推算法を使うのが良いか悩んだ場合は、REFPROPと比較してみるのも一つの手です。

Cranium

インターネットからアクセスできる無料DBではありませんが、Joback先生のCraniumは、各種プロセスシミュレーターへの出力機能も搭載されており、グループ寄与法による様々な物性推算機能が充実していて素晴らしいです。（私が所持しているのは３年以上前のデモソフトなので、今はさらに洗練されているのではないかと思います。）

SRK式

$$p = {\frac{RT}{v-b} - \frac{\alpha(T)a}{v(v+b)}} \tag{1.1}$$ $$\alpha(T) = [1+m(1-\sqrt{Tr})]^2 \tag{1.2}$$ $$m = 0.48+1.574\omega-0.176\omega^2 \tag{1.3}$$

混合則（i成分とj成分の相互作用パラメーター）

$$a = \sum_{i} \sum_{j}x_ix_j(a_ia_j)^{0.5}(1-k_{ij}) \tag{1.4}$$ $$b = \sum_{i} x_ib_i \tag{1.5}$$

$$a_i = 0.42748\frac{R^2T^2_{ci}}{P_{ci}} \tag{1.6}$$ $$b_i = 0.08664\frac{RT_{ci}}{P_{ci}} \tag{1.7}$$

※ωはPitzerの偏心因子。

※以下Soave氏の論文ではaiの係数（Redlich Kwong定数）は0.42747となっておりますが、臨界物性から求めますと、正確には0.42748となります。

Soave,G.;"Equilibrium constants from a modified Redkh-Kwong equation of state"; Chemical Engineering Science, 1972, Vol.27, p.1197-1203.

Redlich Kwong定数の導出はこちらをご参照ください。

本サイトでは、aiは0.42748として計算しております。

SRKの液密度修正推算式例

状態方程式型の推算法では、液密度の推算精度がよくありません。

このため、液密度の推算はAPI法、RACKET法、COSTALD法等がよく用いられますが、ここではSRK式から求まるVに対する修正式としてSRK-Peneloux式をご紹介します。

SRK-Peneloux式は以下になります。

$$V_{correct}^L = \sum_{i=1}^n V_{SRK}^L-0.40768(0.29441-Z_{RA})\frac{RT_{ci}}{P_{ci}}x_i \tag{1.8}$$ $$Z_{RA}=0.29056-0.08775\omega_i \tag{1.9}$$

Peneloux式の推算精度の確認については、こちら（Internet Explorerでのみご覧いただけます）をご参照ください。

上記のリンク先ツールでCalculateボタンを押していただくと、各物性推算法の密度を求めることができます。

※silverlightで作成しております。chrmoeではバージョンによって表示されないので、その場合Internet Exploereでご確認ください

・参考としてモル濃度：Methane:0.3[-]、Ethane:0.3[-]、Proapne:0.4[-]、圧力：1000[kPa]、温度：100[K]の密度計算を確認します。

REFPROPで上記の密度を求めると、642.47[kg/m3]となりますが、SRK-Peneloux式で比較的精度良い結果が得られることが確認できます。

※SRK-Peneloux式の出展

Peneloux A, Rauzy E and Freze R, ; "A consistent correction for Redlich-Kwong-Soave volumes"; Fluid Phase Equilibria,1982, Vol.8, no.1, p.7-23

その他密度の補正計算式として、Claude氏が1993年に発表している補正式も合わせてご紹介します。

Claude F.Leibovici, ; "Variant and invariant properties from cubic equations of state; Fluid Phase Equilibria, 1993, Vol.84, no. 1, p.1-8

SRKのエンタルピー算出

理想気体のエンタルピー

理想気体のエンタルピーは温度の関数で表現されます。

PerryのhandbookやNIST Webbookより、理想気体の比熱を求めるためのパラメーターが掲載されているので、積分することでエンタルピーを求めることができます。

　　

積分してエンタルピーを求めるためには定数項を決める必要があります。定数項の考え方はシミュレーターによって異なります(シミュレーターについてはこちらをご参照ください)が、例えばAVEVA社のPRO/II®、DYNSIM®では、0Cにおける液エンタルピーが0となるように決められています。（理想気体のエンタルピーは0Cにおけるエンタルピーが潜熱となります）※NIST Webbookではエンタルピーも記載されています

Ex.PRO/II®の理想気体エンタルピー係数の確認画面（係数は消しています。温度範囲外になると、外挿されるため注意が必要です）

一方で、例えばAVEVA社のSimCentralでは、25Cにおける理想気体エンタルピーが標準生成熱と一致するようにエンタルピー基準が決められています。

実在気体のエンタルピー

理想気体のエンタルピーと実在気体のエンタルピーの偏倚は以下の式で表されます。

なお、偏倚の式導出は以下の書籍が参考になります。

Integrated Design and Simulation of Chemical Processes

$$\left[h-h^{ideal}\right]_{T,P}=\int_v^\infty\left[P-T\left(\frac{\partial P}{\partial T}\right)_v\right]dv+Pv-RT \tag{1.10}$$

ここで、SRKであれば、圧力は1.1式で表せるため、\(\left(\frac{\partial P}{\partial T}\right)_v\)は、以下となります。

$$\left(\frac{\partial P}{\partial T}\right)_v=\frac{R}{v-b}-\frac{\partial a (T)}{\partial T}\frac{1}{v\left(v+b\right)}$$

よって、1.10式は、以下となります。

$$\left[h-h^{ideal}\right]_{T,P}=\int_v^\infty\left[P-T\frac{R}{v-b}-\frac{\partial a (T)}{\partial T}\frac{1}{v\left(v+b\right)}\right]dv+Pv-RT \tag{1.11}$$ $$\left[h-h^{ideal}\right]_{T,P}=\frac{1}{b}\int_v^\infty\left[\left(\frac{\partial a (T)}{\partial T}T-a (T)\right) \left(\frac{1}{v}-\frac{a}{v+b}\right)\right]dv+Pv-RT \tag{1.12}$$ $$\left[h-h^{ideal}\right]_{T,P}=RT\left(\frac{1}{bRT}\left(\frac{\partial a (T)}{\partial T}\right)\right)\int_v^\infty\left[ln\frac{v}{v+b}\right]dv+Pv-RT \tag{1.13}$$

ここで、a(T)の微分を求めておきます。SRK(1972)のα関数は(1.2)式(以下再掲します)の形ですので、これを代入し、微分していきます。

$$\alpha(T) = [1+m(1-\sqrt{Tr})]^2 \tag{1.2}$$ $$\frac{\partial a(T)}{\partial T} = a\frac{\partial \alpha(T)}{\partial T} \tag{1.14}$$ $$\frac{\partial a(T)}{\partial T} = 2a\sqrt{\alpha (T)}\frac{\partial}{\partial T}\left(1+m\left(1-\sqrt{\frac{T_c}{T}}\right)\right) \tag{1.15}$$ $$\frac{\partial a(T)}{\partial T} = 2a\sqrt{\alpha (T)} \cdot \frac{1}{2} \cdot \left(\frac{-m}{\sqrt{T \cdot T_c}}\right) \tag{1.16}$$ $$\frac{\partial a(T)}{\partial T} = -ma\sqrt{\frac{\alpha (T)}{T \cdot T_c}} \tag{1.17}$$

a(T)の微分\(\frac{\partial a(T)}{\partial T}\)が求まったので、式1.17を式1.13に代入します。

$$\left[h-h^{ideal}\right]_{T,P}=RT\left(\frac{1}{bRT}\left(-maT\sqrt{\frac{\alpha (T)}{T \cdot T_c}}\right)\right)\int_v^\infty\left[ln\frac{v}{v+b}\right]dv+Pv-RT \tag{1.18}$$

これでPVTだけの式になったので、P、TからVを求めてエンタルピーを求めることができます。

上式のままだと計算しづらいので以下少し整理します。

準備中

SRKのエントロピー算出

準備中。

SRKのフガシティー計算

成分iのフガシティーは以下の式より求めることができます。

$$ln \Phi_i = \frac{1}{RT}\int_V^\infty\left[ \left( \frac{\partial P}{\partial n_i} \right)_{T,V,n_j} - \frac{RT}{V}\right]dV-ln(z)$$

SRKの純成分蒸気圧算出

状態方程式法である温度における純成分の蒸気圧を求めるには、液相、気相のフガシティーが等しくなる圧力を繰り返し計算で求める必要があります。

平衡定数の初期値として、よく以下のWilson式が使われます。（臨界温度：Tc、臨界圧力：Pc、標準沸点：NBPが必要です）

準備中。

Wilson式の出典は以下

Wilson, G., “A modified Redlich-Kwong equation of state applicable to general physical data calculations”; 65th AIChE National meeting,1968.

PR式（1976年）

$$p = {\frac{RT}{v-b} - \frac{\alpha(T)a}{v(v+b)+b(v-b)}} \tag{2.1}$$ $$\alpha(T) = {1+m(1-\sqrt{Tr})}^2 \tag{2.2}$$ $$m = 0.37464+1.54226\omega-0.26992\omega^2 \tag{2.3}$$ $$a = \sum_{i} \sum_{j}x_ix_j(a_ia_j)^{0.5}(1-k_{ij}) \tag{2.4}$$ $$b = \sum_{i} x_ib_i \tag{2.5}$$ $$a_i = 0.45724\frac{R^2T^2_{ci}}{P_{ci}} \tag{2.6}$$ $$b_i = 0.0778\frac{RT_{ci}}{P_{ci}} \tag{2.7}$$

Cf)PR式（1978年）

蒸気圧の精度を向上させた1978年の式を以下ご紹介します。

$$p = {\frac{RT}{v-b} - \frac{\alpha(T)a}{v(v+b)+b(v-b)}} \tag{2.8}$$ $$\alpha(T) = {1+m(1-\sqrt{Tr})}^2 \tag{2.9}$$ $$m = 0.37464+1.54226\omega-0.26992\omega^2 (\omega \leqq 0.491) \tag{2.10}$$ $$m = 0.379642+1.48503\omega-0.164423\omega^2 + 0.016666\omega^3 (\omega \gt 0.491) \tag{2.11}$$ $$a = \sum_{i} \sum_{j}x_ix_j(a_ia_j)^{0.5}(1-k_{ij}) \tag{2.12}$$ $$b = \sum_{i} x_ib_i \tag{2.13}$$ $$a_i = 0.457235529\frac{R^2T^2_{ci}}{P_{ci}} \left(1+m_i \cdot \left(1- \sqrt{ \frac{T}{T_{ci}} } \right)\right)^2 \tag{2.14}$$ $$b_i = 0.0777960739\frac{RT_{ci}}{P_{ci}} \tag{2.15}$$

※ここで、\(a_i\)、\(b_i\)の係数は、それぞれ以下の算式より求められています。

$$X = \frac{-1+\sqrt[3]{6\sqrt{2}+8}-\sqrt[3]{6\sqrt{2}-8}}{3} \approx 0.253076587 \tag{2.16}$$

\(a_i\)の係数

$$ \frac{8 \cdot \left(5X+1\right)}{49-37X} \tag{2.17}$$

\(b_i\)の係数

$$ \frac{X}{X+3} \tag{2.18}$$

※PR(1978)式の出展

Peng, D. Y, and Robinson, D. B. ; "The characterization of the heptanes and heavier fractions for the GPA Peng-Robinson programs" 　Gas Processors Association, 1978,

Cf)PR式（1976年）とPR式（1978年）の差異について

偏心因子の大きい成分（アルカンであれば、カーボン数13以上）について、1976式と1978式でどの程度蒸気圧の精度に差異が生じるのか確認してみます。

準備中

PRの液密度修正推算式例

状態方程式型の推算法では、液密度の推算精度がよくありません。

このため、液密度の推算はAPI法、RACKET法、COSTALD法等を用いますが、ここではPR式から求まるVに対する修正式としてPR-Peneloux式をご紹介します。

Peneloux式のvolume補正係をvolume shift parameter推算精度の確認については、こちらをご参照ください。

$$V_{correct}^L = \sum_{i=1}^n V_{PR}^L-0.11537(0.44064-Z_{RA})\frac{RT_{ci}}{P_{ci}}x_i \tag{2.8}$$ $$Z_{RA}=0.29056-0.08775\omega_i \tag{2.9}$$

Peneloux式の推算精度の確認については、こちらをご参照ください。

PRのエンタルピー算出

準備中。

PRのエントロピー算出

準備中。

状態方程式法は式変形によってz、あるいはvの３次方程式に変形することが可能です。

具体的な式変形の流れは以下をご参照ください。

例としてSRK式を３次式の形に変形していきます。(1.1)式からスタートし、できるだけ式を省略せずに以下記載します。

$$p = {\frac{RT}{v-b} - \frac{\alpha(T)a}{v(v+b)}} \tag{4.1}$$

両辺に(v-b)v(v+b)をかけます。

$$p(v-b)v(v+b) =RTv(v+b) - \alpha(T)a(v-b) \tag{4.2}$$ $$pv^3-pb^2v-RTv^2-bRTv + \alpha(T)av-\alpha(T)ab =0 \tag{4.3}$$ $$pv^3-RTv^2+\left(-pb^2-bRT + \alpha(T)a\right)v-\alpha(T)ab =0\tag{4.4}$$

両辺に\(\frac{p^2}{R^3T^3}\)をかけます。さらに、\(\frac{pv}{RT}=z\)を使って、式変形します。

$$z^3-z^2+\left(\frac{-p^2b^2}{R^2T^2}-\frac{bp}{RT} + \frac{\alpha(T)ap}{R^2T^2}\right)z-\frac{\alpha(T)aP}{R^2T^2}\frac{bP}{RT} =0\tag{4.5}$$

ここで、\(\frac{\alpha(T)aP}{R^2T^2}=A\)、\(\frac{bp}{RT}=B\)とすると、

$$z^3-z^2+\left(-B^2-B+A\right)z-AB =0\tag{4.6}$$

大分スッキリした形になりました。A、Bはa,b,R,Tから求められますので、後はこの３次方程式を解くだけです。

３次方程式の解法については、非線形方程式の解法をご参照ください。

VBAのページでも実例を掲載していこうと思います。

主なアルファ関数を以下ご紹介します。

RK(1949)

$$\alpha (T)=\frac{1}{\sqrt{T}}$$

Wilson(1966)

$$\alpha (T)=\left[T_r+\left(1.57+1.62\omega \right)\left(1-T_r\right)\right]$$

SRK(1972)

$$\alpha (T)=\left[1+m\left(1-T_r^{0.5}\right)\right]$$

※mについては、こちらをご確認ください。

Soave(1993)

Lee-Kesler(1975)式で各Tr、ωで蒸気圧が等しくなるように係数を決めた式

※Lee-Kesler方のPitzer式は、NBP～超臨界域の推算精度は良いが、対臨界温度が低い領域での推算精度が著しく低下する、、、そうです。一度確認してみないと実感がわかないですが。

$$\alpha (T)=1+m\left(1-T_r\right)+n\left(1-T_r^{0.5}\right)^2$$ $$m=0.484+1.515\omega-0.44\omega^2$$ $$n=2.756m-0.700$$

Twu et al(1995)：以下の論文によります

$$\alpha (T)=T_r^{N\left(M-1\right)}e^L\left(1-T_r^{NM}\right)$$

※α関数確認のソースは以下論文になります。（Part1はPeng-Robinson用）

Chorng H. Twu, John E. Coon, and John R. Cunningham; "A NEW GENERALIZED ALPHA FUNCTION FOR A CUBIC EQUATION OF STATE PART 2. REDLICH-KWONG EQUATION"; Fluid Phase Equilibria,1995, p.61-69

SRKの修正式としてTwuのα関数を用いた場合にどの程度精度が変わるのか、以下確認してみました。

上述の論文で、L,M,Nのパラメーターリストとして、Argon、Benzene、Cyclohexaneや主要なハイドロカーボンのデータがあります。

まずはmethaneについて確認してみます。

methaneのパラメーターとして次の論文中の数値を使用します。 Tc:190.58[K] 46.04[bar] L:0.106750[-] M:0.920161[-] N:3.09674[-]

準備中。

SRK、PRの混合則は、非理想性の高い成分の組み合わせには適していません。

主な修正混合則を以下ご紹介します。

Panagiotopoulos-Reid Mixing Rule （1985）

$$a=\sum_i \sum_j y_i y_j a_{ij}$$ $$a_{ij}=\sqrt{a_i a_j}\left[1-k_{ij}+(k_{ij}-k_{ji})x_i\right]$$

BWRS式（1972年）

Virial型の状態方程式の例として、BWRS式をご紹介します。

BWRS式は、軽炭化水素の物性推算に適した推算法で、重質炭化水素や、極性の強い物質の物性推算には適していません。

$$P = \rho RT+ \left( B_0RT-A_0-\frac{C_0}{T^2}+\frac{D_0}{T^3}-\frac{E_0}{T^4} \right) \rho ^2 + \left( bRT-a-\frac{d}{T} \right) \rho ^3 $$ $$+ \alpha \left( a + \frac{d}{T}\right) \rho^6 + \frac{c\rho^3}{T^2} \left(1+\gamma \rho^2 \right) exp \left(-\gamma \rho^2\right) \tag{5.1}$$

Cf)BWR式（1940年）

$$P = \rho RT+ \left( B_0RT-A_0-\frac{C_0}{T^2}\right) \rho ^2 + \left( bRT-a \right) \rho ^3 $$ $$+ a \alpha \rho^6 + \frac{c\rho^3}{T^2} \left(1+\gamma \rho^2 \right) exp \left(-\gamma \rho^2\right) \tag{5.2}$$

BWRS式における各パラメーター値が入手できない場合、偏心因子、臨界体積、臨界温度から求められます。

$$B_0=\frac{0.443690+0.115449\omega}{\rho_c}$$ $$A_0=\frac{\left(1.28438-0.920731\omega\right)RT_c}{\rho_c}$$ $$C_0=\frac{\left(0.356306+1.70871\omega\right)RT_c^3}{\rho_c}$$ $$D_0=\frac{\left(0.0307452+0.179433\omega\right)RT_c^4}{\rho_c}$$ $$E_0=\frac{\left(0.006450-0.022143\omega exp\left(-3.8\omega\right) \right)RT_c^5}{\rho_c}$$ $$b=\frac{0.528629-0.349261\omega}{\rho_c^2}$$ $$a=\frac{\left(0.484011+0.754130\omega \right)RT_c}{\rho_c^2}$$ $$d=\frac{\left(0.0732828+0.463492\omega \right)RT_c^2}{\rho_c^2}$$ $$c=\frac{\left(0.504087+1.32245\omega \right)RT_c^3}{\rho_c^2}$$ $$\alpha=\frac{0.0705233-0.044448\omega}{\rho_c^3}$$ $$\gamma=\frac{0.544979-0.270896\omega}{\rho_c^2}$$

※ただし、English単位系なので、注意。R=10.73[psi・ft3/(R・lb-mol）]

以下、ハロゲン化炭化水素の物性推算にも良いという記載があったので、試しに以下のペーパーに書かれているR11、R12、R13、R14、R22、R23、R113、R114について、BWRSでどの程度の精度が出るのか、REFPROPの計算結果と比較して確認してみました。

K. H. Aboul-Fotouh and K. E. Starling.; "USE OF A GENERALIZED MODIFIED BWR EQUATION OF STATE FOR HALOGENATED HYDROCARBON SATURATED THERMODYNAMIC PROPERTIES"; 1978,

詳細はこちらをご参照ください。

BWRS式は、SRKや、PRのように解析解を求めることができないので（数学に強い方なら解けるのかもしれませんが、、、）、収束計算で求めました。

BWRS式は、解から離れるとあっという間に発散してしまい、逐次代入法では全く収束しないため、Steffensen法で解いています。

ただ、Steffnesen法を用いても初期値が悪いとやはり収束しなかったので、やむをえず、一旦SRK式で密度を求め、その密度を初期値として与えて収束計算を行っています。

もっと上手い方法をご存知の方がいらっしゃいましたら、是非教えてください

使用したパラメーターは以下。

検証結果（一部）は以下。

REFPROPの適用範囲の制約もあり、暫定なので検証の圧力、温度がまばらですが、、、。

時間ができたらC#でBWRSの推算ツールも作成してみます。

Thermodynamics: Fundamentals for Applicationsで活量係数モデルの考え方がステップバイステップで解説されているので、是非ご一読ください。

式の導出も非常に丁寧になされており、全部載せてしまいたいところですが、勝手に著書の式を全て転載するわけにはいかないので、一部だけ抜粋し、他の部分は考え方だけとして以下ご紹介します。

液相活量係数モデルの一番シンプルな出発点として、過剰Gibbsエネルギーが組成変化の影響のみによって変わると仮定します。

等温、等圧下において(x1-x2)周りでテイラー展開することで以下のRedlich-Kisterの展開式を得ます。

$$ \frac{G^E}{RT}= x_1x_2[A + B(x_1-x_2) + ...] $$

ここで各パラメーターは温度のみに依存する形となっています。（液に対しては圧力の影響は小さいと考えられる）

過剰Gibbsエネルギーの組成に対する式形式が２次関数に近い範囲においては、１次展開の項までで十分ですが、より高次の複雑な関係性を持つ場合は、より高次の項まで計算する必要があります。

まず上記の式の考え方を出発点として見ておくと、以降の各液相活量係数モデルの式展開が入ってきやすくなるかと思います。

上述の著書では第１項以降を無視したPorter式やより3次以降についての式についても記載があります。Redlich-Kisterの展開式に基づく推算式は、いずれにしても多成分系への適用や水素結合等を有するような非理想系への適用が難しいので、Margules式だけ確認すれば十分かと思います。

Margules式(3-suffix Margules式)

前出のReflich-Kisterの展開式において、第２項以降を無視し、A+B=\(A_{21}\)、A-B=\(A_{12}\)を用いて下式を得ます。

$$ln \gamma_1= x_2^2[A_{12} + 2(A_{21}-A_{12})x_1]$$ $$ln \gamma_2= x_1^2[A_{21} + 2(A_{12}-A_{21})x_2]$$

なお、活量係数と過剰Gibbs energyの関係式として以下を用いています。

$$ ln \gamma_i = \left[\frac{\partial (nG^E / RT)}{\partial n_i} \right]_{T,P,n_j}$$

cf)Perry's Engineering Handbook 8ed

vanLaar式 $$ln \gamma_1= \frac{A_{12}}{\left(1 + \frac{A_{12}x_1}{A_{21}x_2}\right)^2}$$ $$ln \gamma_2= \frac{A_{21}}{\left(1 + \frac{A_{21}x_2}{A_{12}x_1}\right)^2}$$

半経験モデルとして、局所モル分率に基づくWilson式を紹介します。

DECHEMAの式形

$$ln\gamma_i=1-ln\sum_{j=1}x_j\lambda_{ij}-\sum_{k=1}\frac{\displaystyle x_k\lambda_{ki}}{\displaystyle \sum_{j=1}x_j\lambda_{kj}}$$ $$\lambda_{ij}=\frac{v_i^L}{v_j^L}exp\left[-\frac{\lambda_{ij}-\lambda_{ii}}{RT}\right]$$ $$A_{ij}=(\lambda_{ij}-\lambda_{ii})$$

ただし、R=1.98721[kcal/mol-K]

液液平衡計算は取り扱えない。

Wilson式の出典は以下

Wilson,GM.; "Vapor-Liquid Equilibrium XI. A New Expression for the Excess Free Energy of Mixing"; J Amer Chem Soc, 1964, 86, p.127-130.

Excelを使った計算例はこちらをご参照ください。

DECHEMAの式形

$$ln\gamma_i=\frac{\displaystyle \sum_{j=1} \tau_{ji} G_{ji}x_j}{\displaystyle \sum_{k=1}G_{ki}x_k}+\sum_{j=1}\frac{\displaystyle x_j G_{ij}}{\displaystyle \sum_{k=1}G_{kj}x_k}\left(\tau_{ij}-\frac{\displaystyle \sum_{j=1} \tau_{kj}G_{kj}x_k}{\displaystyle \sum_{k=1}G_{kj}x_k}\right)$$ $$\tau_{ij}=\frac{g_{ij}-g_{jj}}{RT}$$ $$A_ij=(g_{ij}-g_{jj})$$

ただし、R=1.98721[kcal/mol-K]

上記の式形ですと、ある特定の温度におけるパラメーターで計算を行う場合はよいのですが、あるレンジ内で使えるパラメーターにしようと思うと、パラメーター数としては不十分な場合があります。

NRTLの場合、Simulatorrによって異なりますが、以下のような式形で表現されていることが多いかと思います。

$$\tau_{ij}=a_{ij}+\frac{b_{ij}}{T}+\frac{c_{ij}}{T^2}+d_{ij}ln(T)+e_{ij}T+f_ijTln(T)$$ $$G_ij=exp\left(-A{ji} \tau_{ij}\right)$$ $$A_{ji} = \alpha_{ji}+\beta_{ji}$$

この場合、DECHEMAの式の\(A_{ij}:[cal/mol]\)を、Simulatorの単位系に合わせる必要があります。

圧力一定の場合の計算例はこちらをご参照ください。

NRTL式の出典は以下

HRenon, H. and Prausnitz, J. M.; "Local Composition in Thermodynamic Excess Functions for Liquid Mixtures", AIChE J.,1968, vol.14, p.135-144.

上記論文には、用いる流体性状の組み合わせに応じて、推奨されるαの値が記載されているので、実験データに合うようにパラメーターを回帰する際には参考にしてみてください。

Pythonを使った計算例はこちらをご参照ください。

Excelを使った計算例はこちらをご参照ください。

回帰を行う場合の注意点については、こちらをご参照ください。

なお、フリーソフトと市販シミュレーターで紹介したSimCentralでは、上式のバイナリパラメーターの変更が非常に見やすいGUIで可能となっています。（数値は消しています）

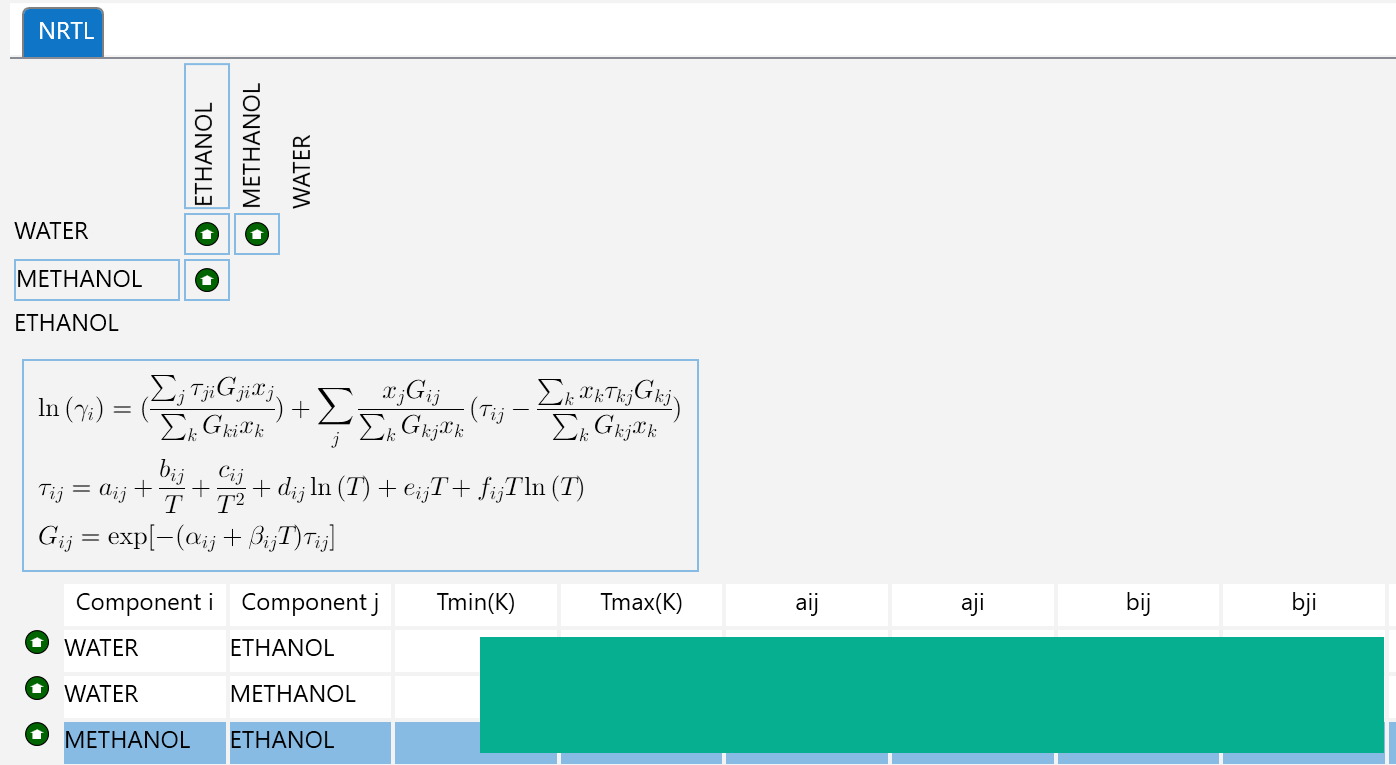
UNIQUACの式は、分子の大きさ、形状差を考慮に入れたcombinational termと、分子間相互作用を考慮したresidual term combinational termで表現されます。

$$ \frac{g^{E}}{RT} = \frac{g^{E}_{combinational}}{RT} + \frac{g^{E}_{residual}}{RT}$$

本ページでは式を記載しておりませんので、詳細はPerryのEngineering handbookをご参照ください。

以下、計算例のみ記載いたします。

ツールでの比較

Wilson, NRTLの比較はこちらに計算ツールを作成しました。

※現状VLE（温度固定）のみです。

Wilsonのパラメーターは、以下の式形で搭載しています。

$$\lambda_{ij}=\frac{v_i^L}{v_j^L}exp\left[-\frac{\lambda_{ij}-\lambda_{ii}}{RT}\right]$$ $$A_{ij}=a_{ij}+\frac{b_{ij}}{T}$$

NRTLのパラメーターは、以下の式形で搭載しています。

$$\tau_{ij}=a_{ij}+\frac{b_{ij}}{T}+c_{ij}+d_{ij}ln(T)+e_{ij}T+f_ijTln(T)$$ $$G_ij=exp\left(-A{ji} \tau_{ij}\right)$$ $$A_{ji} = \alpha_{ji}+\beta_{ji}$$

ツールの使い方は、以下のように、計算温度、刻みを入力してCalcボタンを押すだけです。

※2016/10/8現在、各パラメーターのユーザー入力には対応しておりません。（水-ethanolのみ）

原子団寄与法による推算について：原子団寄与法による各種物性（標準沸点、臨界物性等）の求め方、及び比較結果をまとめていきます。PRO/II、DYNSIMやSimCentral等のシミュレーターをお使いの方は、TDMからこうした物性推算機能を呼び出すことが可能です。詳細はソフトウェアベンダーにお問い合わせください。

以下の本が参考になります。

Jobakの推算法

Lydersenの原子団寄与法に基づいた推算法

標準沸点、臨界温度、臨界圧力の推算

$$T_{b}(K) = 198 + \Sigma (vck)$$ $$T_{c}(K) = T_{b} \left[ 0.584 + 0.965{\sum_{k} N_{k}(tck)} - {\sum_{k} N_{k}(tck)}^2 \right]^{-1}$$ $$P_{c}(bar) = \left[ 0.113 + 0.0032 N_{atoms} - {\sum_{k} N_{k}(pck)} \right]^{-2}$$ Wilson-Jaspersonの推算法

標準沸点、臨界温度、臨界圧力の推算

$$T_{b}(K) = 204.359 ln \left[ \sum_{k} N_{k}(tblk) + W \sum_{j} M_{j}(tb2j) \right]$$ $$T_{c}(K) = T_{b}\left[0.048721 - 0.019846N_r + {\sum_{k} N_{k}(\Delta tck)} + \sum_{j} M_{j}(\Delta tcj)\right]^{0.2}$$ $$P_{c}(bar) = 0.0186233 \cdot T_c / \left[ -0.96601 + exp(Y) \right] $$ $$Y = -0.0092295-0.0290403 \cdot N_r + 0.041 \left[ \sum_{k} N_{k}(\Delta pck) + \sum_{j} M_{j}(pcj) \right]$$ Marrero-Pradilloの推算法

標準沸点、臨界温度、臨界圧力の推算

$$exp(T_b/T_{b0}) = \sum_{i} N_{i}T_{b1i} + \sum_{j} M_{j}T_{b2j} + \sum_{k} M_{k}T_{b3k} $$ $$exp(T_c/T_{c0}) = \sum_{i} N_{i}T_{c1i} + \sum_{j} M_{j}T_{c2j} + \sum_{k} M_{k}T_{c3k} $$ $$(P_c-P_{c1})^{-0.5} = \sum_{i} N_{i}P_{c1i} + \sum_{j} M_{j}P_{c2j} + \sum_{k} M_{k}P_{c3k} $$

出典

J.Marrero,R.Gani,"Group-contribution based estimation of pure component properties",Fluid Phase Equilibria,2001, p.183–p.208

Constantinou-Ganiの推算法

標準沸点、臨界温度、臨界圧力の推算

$$T_{b}(K) = 204.359 ln \left[ \sum_{k} N_{k}(tblk) + W \sum_{j} M_{j}(tb2j) \right]$$ $$T_{c}(K) = 181.128 ln \left[ {\sum_{k} N_{k}(tclk)} + W \sum_{j} M_{j}(tc2j)\right]$$ $$P_{c}(bar) = \left[ {\sum_{k} N_{k}(pclk)} + W \sum_{j} M_{j}(pc2j) + 0.10022 \right]^{-2} + 1.3705 $$

各推算法の精度

構造異性体を考慮できるのはMarrero-Pradilloの推算法だけですが、以下各推算法について、o-xylenの各物性について、DIPPRのデータと比較してみます。

Jobakの推算法

標準沸点の推算用係数

	Nk	tbk	Nk(tbk)
CH	4	26.73	106.92
CH3	2	23.58	47.16
C	2	31.01	62.02

臨界温度、臨界圧力の推算用係数

	Nk	tck	pck	Nk(pck)	Nk(pck)
CH	4	0.0082	0.0011	0.0328	0.0044
CH3	2	0.0141	-0.0012	0.0282	-0.0024
C	2	0.0143	0.0008	0.0286	0.0016

推算結果

	Jobak	DIPPR	Error %
Tb[K]	414.10	417.58	0.84
Tc[K]	625.1	630.3	0.83
Pc[K]	35.86	37.32	4.08

Wilson-Jaspersonの推算法

標準沸点の推算用係数

	Nk	tbk	Nk(tbk)
ACH	4	0.9297	3.7188
ACCH3	2	1.9669	3.9338

臨界温度、臨界圧力の推算用係数

	Nk	tck	pck	Nk(pck)	Nk(pck)
C	8	0.008532	0.72983	0.068256	5.83864
H	10	0.002793	0.1266	0.02793	1.266

推算結果

	Wilson	DIPPR	Error %
Tb[K]	415.90	417.58	-0.40
Tc[K]	630.8	630.3	0.08
Pc[K]	36.49	37.32	-2.27

Constantinou-Ganiの推算法

標準沸点、臨界温度、臨界圧力の推算

標準沸点の推算用係数

	Nk	tbk	Nk(tbk)
ACH	4	0.9297	3.7188
ACCH3	2	1.9669	3.9338

臨界温度、臨界圧力の推算用係数

	Nk	tck	pck	Nk(pck)	Nk(pck)
ACH	4	3.7337	0.0075	14.9348	0.03
ACCH3	2	8.213	0.0194	16.426	0.0388

推算結果

	CG	DIPPR	Error %
Tb[K]	415.90	417.58	0.41
Tc[K]	624.1	630.3	1.00
Pc[K]	36.37	37.32	2.60

Marrero-Pradilloの推算法

標準沸点の推算用係数

	Nk	tbk	Nk(tbk)
ACH	4	0.8365	3.346
ACCH3	2	1.5653	3.1306

臨界温度、臨界圧力の推算用係数

Marrero-Pradilloの推算法では、構造異性体も考慮することが可能です。結合箇所に応じて第２項までパラメーターが用意されています。以下のテーブルは第１項、第２項の計算結果を積算した値です。

	Nk	tck	pck	Nk(pck)	Nk(pck)
aCH	4	2.0337	0.00726	8.1348	0.02904
aC-CH3	2	3.4611	0.020907	6.9222	0.041814

推算結果

	MP	DIPPR	Error %
Tb[K]	410.22	417.58	1.76
Tc[K]	622.2	630.3	1.29
Pc[K]	36.72	37.32	1.61

以下粘度、熱電伝度、拡散係数の推算において、主にChapman-Enskogの式を用いますが、その際Lennard-Jonesパラメーターが必要となります。パラメーターが得られない場合の推算式を以下紹介します。

なお、The Properties of Gases and Liquidsでは注意点として、極性物質についてはLennard-Jonesパラメーターのみでは不十分であることが述べられており、Brokawの補正式が紹介されていますので、極性物質の推算を行う場合は、ご注意ください。

$$ \sigma \left(\frac{p_c}{T_c} \right)^{1/3} = E-10(2.3551-0.087) $$ $$ \frac{\epsilon / k_B}{T_c} = 0.7915 + 0.16930 $$

ここで、\(p_c\)：臨界圧力[atm]、\(p_c\)：臨界温度[K]、\( \omega \)：偏心因子[-]、\(\sigma\)：衝突直径[m]です。

上式の参考書籍は以下になります。なお、以下の参考書籍のAppendixに主な気体のLennard-Jonesパラメーターが記載されています。

例えば上記の書籍に記載されているH2のパラメーターについて精度を確認してみます。

NISTのWebbookから、Tc : 33.18[K]、Pc[bar]を使って\(\sigma\)を求めると、3.113e-10。

一方で上記書籍の数値は\(\sigma\)=2.827e-10ですので誤差10%程度です。

また、\(\epsilon / k_B \)については、推測値：31.9に対し、上記書籍記載の数値は59.7ですので、こちらは90%近い誤差が生じています。

Lennard-Jonesパラメーターについては極力文献値等を探した方が良さそうです。

上述の参考書籍には以下４つの前提条件が記載されています。以降のChapman-Enskogの式を採用する場合、念頭に置いてください。

1.気体が十分に希薄で、２分子間の衝突のみが想定できること

2.衝突時の分子運動は古典力学で表現できること

3.全ての衝突が弾性衝突であること

4.分子間の相互作用は分子間の中心のみで考えられること

低圧域の粘度推算：Chapman-Enskogの式（1916）

$$ \mu = 2.6693E^{-26} \left( \frac{(MT)^{1/2}}{\sigma^2 \Omega^*} \right)$$

ここで、\( \mu \)：粘度[Pa/sec]、M：分子量、\(\sigma\)：衝突直径[m]、 \(\Omega^*\)：還元衝突積分(reduced collision integral)

ここで、還元衝突積分は無次元温度：\(T^* = T/ (\epsilon / k_B) \)の関数となっている。ただし、\(k_B\)：ボルツマン定数（1.3806504×E-23[J/K]）、\( \epsilon \)：特徴的な結合エネルギー(characteristic energy of interaction)。無次元温度の適用範囲は、0.3～100。

例題14.1で空気の粘度が計算されており、313.15Kの１点データとはいえ、誤差0.4%と精度が良いことが示されています。

衝突積分は上記の参考書籍のAppendixより、下式で表されます。

$$\Omega^* = \frac{1.16145}{(T^*)^{0.14874}} + \frac{0.52487}{exp(0.77320 \cdot T^*)} + \frac{2.16178}{exp(2.43787 \cdot T^*)}$$

また、0.4 <\( T^* \) <1.4においては、以下の簡易式も紹介されています。

$$\Omega^* = \frac{1.1604}{(T^*)^{0.5}} $$

H2しか確認していませんが、無次元温度が上記の範囲内であれば十分な精度がありそうです。

参考

Chung TH, Ajlan M, Lee LL, Starling KE, "Generalized multiparameter correlation for nonpolar and polar fluid transport properties.", Ind Eng Chem, 1988, 27, 671-9.

粘度の混合測

熱伝導度推算

Chapman-Enskogの式

$$ k = 8.3224E^{-22} \left( \frac{(T/M)^{1/2}}{\sigma^2 \Omega^*} \right)$$

ここで、熱電導度：k[W/m-K]。その他のパラメーターについては粘度の項をご参照ください。

熱伝導度の混合測

相互拡散係数推算

$$ D = D_{AB} = D_{BA} = 1.8829E^{-22} \frac{ \{T^3 \left[ (1/M_A) + (1/M_B) \right] \}^{1/2} }{p \sigma_{AB}^2 \Omega_D}$$

ここで、衝突積分は上記の参考書籍のAppendixより、下式で表されます。

$$\Omega^* = \frac{1.06036}{(T^*)^{0.15610}} + \frac{0.19300}{exp(0.47635 \cdot T^*)} + \frac{1.03587}{exp(1.529 \cdot T^*)}　+ \frac{1.76474}{exp(3.89411 \cdot T^*)}$$

拡散係数については、上記の‘Chapman-Enskogの式以外にも、例えばThe Properties of Gases and Liquidsでは、Wilke-LeeやFullerの方法が紹介されています。

こちらの本では、上述の３つの方法の精度について、CO2、N2の実験結果との比較を行っていますが、いずれの方法も大きな差異はなく、いずれもそれなりの精度がありそうです。（ただ、注意点として、あくまで上記の例はデータバンクのある成分同士の比較であって、アミンではどの程度の精度が出るか分からないと記載されています。）

$$ D_{AB} = \frac{7.4e^{-8}(\phi M_B)^{1/2}T}{\eta_B V_A^{0.6}} $$

ここで、\( D_{AB}\)はB溶液中における溶質Aの相互拡散係数[cm/s]、\(M_B\)は溶液Bの分子量[g/mol]、\( \eta_B \)は溶液Bの粘度[cP]、\(V_A\)は溶質Aの標準沸点における分子容量[cm3/mol]、\(\phi \)は溶液Bの会合係数になります。

会合係数は、溶液が水の場合2.6、メタノールで1.9、エタノールで1.5、会合を起こさない場合は1.0です。

The Properties of Gases and LiquidsのExample11-5に水とエチルベンゼンの相互拡散係数に関する例が記載されており、実験データとして293Kにおいて、\(D_{AB} = 0.81*10^-5 cm^2/s \)(Witherspoon and Bonoli, 1969)となっています。拡散係数の計算に必要な上述データは「各種物性DBへのリンク」で紹介した各種リンクより入手可能ですので、検証してみてください。こちらの例では上述の実験データに対して誤差-5%程度となります。

以下Twuの推算方法をご紹介します。

Chorng H. Twu ; "An internally consistent correlation for predicting the critical properties and molecular weights of petroleum and coal-tar liquids" 　Fluid Phase Equilibria, 1984, 16, 137-150

Twuの推算法では、比重、標準沸点、分子量の内、２つ情報があれば、その他の物性（臨界物性、偏心因子、左記３つの物性の内の残り１つ）を推算することができます。

以下、主なハイドロカーボンに対して、比重、標準沸点から他の物性について、Excelで精度を確認してみます。

前準備

臨界温度

$$ T_c^0 = T_b * (0.533272 + 0.191017 \cdot 10 ^ {-3} \cdot Tb + 0.779681 \cdot 10 ^ {-7} \cdot Tb ^ 2 $$ $$ - 0.284376 \cdot 10 ^ {-10} \cdot Tb ^ 3 + 0.959468 \cdot 10 ^ {28} \cdot Tb ^ {-13}) ^ {-1}$$

臨界圧力

$$ P_C^O = (3.83354 + 1.19629 \cdot \alpha ^ {0.5} + 34.8888 \cdot \alpha + 36.1952 * \alpha ^ 2 + 104.139 \cdot \alpha ^ 4) ^ 2$$

ただし、\(\alpha=1-T_b/T_c^0 \)。

臨界体積

$$ V_C^O = (1 - (0.419869 - 0.505839 \cdot \alpha - 1.56436 \cdot \alpha ^ 3 - 9481.7 \cdot \alpha ^ {14})) ^ {-8}$$

比重

$$ SG^O = 0.843593 - 0.128624 \cdot \alpha - 3.36159 \cdot \alpha ^ 3 - 13749.5 \cdot \alpha ^ {12}$$

分子量

$$T_b = \exp{(5.71419 + 2.71579 \cdot X - 0.28659 \cdot (\theta ^ 2) - 39.8544 / \theta - 0.122488 / (\theta ^ 2))} $$ $$ - 24.7522 \cdot \theta + 35.3155 \cdot (\theta ^ 2)$$

\(\theta\)を求めるには収束計算が必要ですので、ここではVBAでNewton法を使って求めます。

$$ \theta = ln (MW^0)$$ 前準備で求めたパラメーターから各物性の推算

臨界温度

$$ T_c = T_c^0 \cdot ((1 + 2 \cdot f_T) / (1 - 2 \cdot f_T)) ^ 2$$ $$ f_T = \Delta SG_T * (-0.362456 / (T_b ^ 0.5) + (0.0398285 - 0.948125 / (T_b ^ {0.5})) \cdot \Delta SG_T)$$ $$ \Delta SG_T = \exp(5(SG^0-SG))-1 $$

臨界圧力

$$ P_c = P_C^O \cdot (T_c / T_c^0) \cdot (V_C^O / V_c) \cdot ((1 + 2 \cdot f_p) / (1 - 2 \cdot f_p)) ^ 2 $$ $$ f_p = \Delta SG_P \cdot (2.53262 - 46.1955 / (T_b ^ {0.5}) - 0.00127885 * T_b + (-11.4277 + 252.14 / T_b ^ {0.5} $$ $$+ 0.00230535 * T_b) * \Delta SG_P) $$

臨界体積

$$ V_c = V_C^O * ((1 + 2 \cdot f_v) / (1 - 2 \cdot f_v)) ^ 2 $$ $$ f_v = \Delta SG_V \cdot (0.46659 / T_b ^ {0.5} + (-0.182421 + 3.01721 / T_b ^ {0.5}) \cdot \Delta SG_V) $$

分子量

$$ ln (MW) = Log(MW_0) \cdot ((1 + 2 \cdot f_M) / (1 - 2 \cdot f_M)) ^ 2 $$ $$ f_M = \Delta SG_M * (| x | + (-0.0175691 + 0.193168 / T_b ^ {0.5}) * \Delta SG_M) $$ $$ |x| = | 0.0123420 - 0.328086 / T_b ^ {0.5} | $$ $$ \Delta SG_M = \exp(5(SG^0-SG))-1 $$

MWの\(\theta\)の計算については、ブログを確認してください。エクセルでn-アルカンの物性を、Perryのengineering bookに記載されているSG、NBPから推算し、結果をやはりPerryの同著の数値と比較した結果が以下になります。

分子量の大きい成分の臨界体積と、一部臨界圧力のズレが大きくなっているものの、その他の物性については、誤差1%以下で精度としは問題無さそうです。

蒸気の推算は、比重、標準沸点からその他の物性を推算しましたが、もし入力した比重、標準沸点に誤差があった場合、最終的な計算結果にどの程度の影響を与えるでしょうか。

以下、比重、標準沸点にわざと数%の誤差を与えて、計算結果の誤差を確認してみます。

準備中。

簡単ですが、上記の推算ツールを作成しました。（2016/08/27:Internet Explorerのみ対応）

使い方は以下のようにNBP(K)、SGを入力し、Calculateを押すだけです。