プラントデータ、シミュレーションデータの取り扱い
このページではプラントの生データの前処理や解釈、シミュレーションへのデータ入力や結果解釈等についてまとめていきます。
データの収集
データ処理の練習をする上で、練習用のデータをどうやって用意するかという問題があります。プラントの生データにアクセスすることができればベストですが、生データが無い場合、仮想のデータセットを用意する上でいくつかのアプローチがあるかと思います。以下、いくつかの方法をご紹介します。
回帰計算
ExcelのソルバーやPythonの最適化を使った回帰計算例、回帰計算の注意点等を整理していきます。
回帰計算の基本的をまとめていきます。(作成中)
scikitlearnのOPTICSを使って、以下の仮想プラントデータをロード毎に分類していきます。
実用的な回帰計算例として、バイナリーパラメーターの回帰計算例をご紹介します。違いを見やすくするために、ほぼ理想状態のバイナリーパラメーターからスタートし、水-エタノールの回帰を行います。
実験データと計算上の値との自乗誤差を積算し、誤差が最小となるパラメーターをExcelのソルバーで求めます。
以下はwater-methanolの例になります。
(NRTLの詳細については、こちらを参照ください)
scipy.optimizeのleastsqやcurve_fitを使っていきます。
シミュレーションの注意点にも少し記載しましたが、回帰計算を行う場合には、元データがどのような性状のものであるかを事前に確認することが重要です。
以下に示すアンスコムの例は、回帰を行う際の注意点として念頭に置いておいた方が良いかと思います。
こちらの本が非常に参考になります。
アンスコムの例も紹介されていますが、他にも回帰をする上での注意点が分かりやすくまとめられています。
他にもあり勝ちな問題として、「誤差を小さくするために次数を上げすぎてしまうこと」は機械学習でも過学習として取り上げられることがありますが、特にプラントのデータにはそもそもの測定誤差がありますので、外挿範囲の問題だけではなく、ノイズを含んだ値に合わせこみすぎることで本来の値とのズレが逆に大きくなってしまう懸念があります。
ホワイトノイズについては後述の移動平均等でなまして除去することも考えられます。
シミュレーション前のデータ処理
プロセスシミュレーションを行う前に考慮しておいた方が良いポイントをまとめていきます。特に整合性の取れたデータを使うために必要なData Reconciliationや、各種フィルタリング方法についてまとめていきます。
プラントの計器から送られてくる生データは、計器の誤差やホワイトノイズ、触媒劣化や閉塞等によるプラントの長期的な変動等、バランスを取る上で邪魔な要素が多くあります。定常シミュレーションはマテバラ、ヒートバラが取れていることを前提としているため、生値をそのままただプロセスシミュレーターに流しこむとバランスが取れていないため収束させることができません。このため、事前にData Rconciliationを行います。
Data Rconciliationでお勧めの本は、Data Reconciliation and Gross Error Detection、Data Processing and Reconciliation for Chemical Process Operations、Dynamic Data Reconcilationです。Amazonでの評価は高くないですし、確かに実用的かと言われると、そのまま実プラントで使えるわけではないですが、考え方を理解するには私は良い本だと思っています。後段で、上述の著書で紹介されているいくつかのフィルタリング手法についても触れたいと思います。
上述のように、プラントの生データは、流量計の誤差や成分分析の測定誤差等から、そのままではマテバラが取れていません。
また、定常状態が取れている状態でのサンプリングができているか、もし完全には定常状態とはいえない場合はホールドアップ分の時間差の考慮、サンプリング後の分析精度も考慮する必要があります。
プロセスシミュレーターで計算を行う前に、マテバラが取れたデータを用意する必要がありますので、以下Excelを使う方法、Pythonを使う方法、Simulinkを使う方法、シミュレーターを使う方法等をご紹介します。
前段でご紹介した本では計器誤差のタイプとして、大きくRandom ErrorとGross Errorに分けて紹介されています。
Random Error Gross Error前段でご紹介した本で紹介されているいくつかのフィルタリング手法をご紹介します。
まず、以下がフィルタリング前の真の値と生値のトレンドになります。
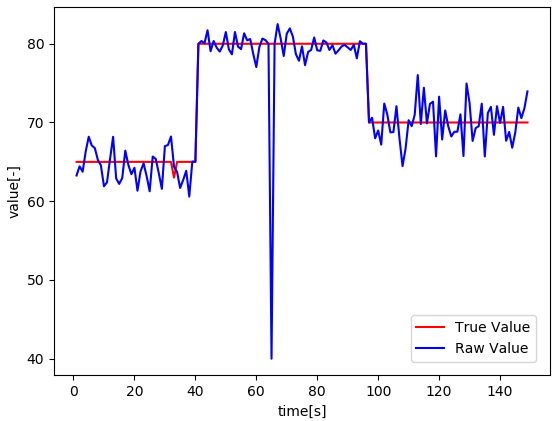
こちらのデータを元に、各フィルタリング手法を適用した場合の真の値との絶対誤差を時間軸に向かって積分していく、Integral Absolute Error(IAE)で評価していきます。
指数フィルタ残念ながら、上述の本で記載されている指数フィルタの式がおかしいので注意が必要です。
以下指数パラメーターが0.1、0.4の場合のグラフを表示しています。
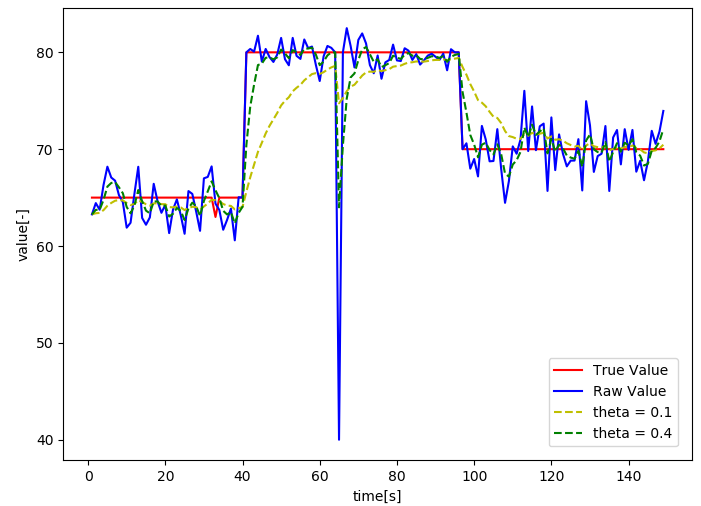
生値vs真値、生値vsΘ=0.1、生値vsΘ=0.4のIAEをそれぞれ比較すると、262.43、306.25、183.95となっています。
Θが小さすぎると、ステップ変化に対する時間遅れによる誤差の累積が大きくなりすぎてしまいますし、Θが大きすぎると、今度は生値vs真値の誤差と同じになってしまいます。
また、ここではノイズの除去性能を高めると同時に、時間遅れを軽減する非線形指数フィルタも紹介されています。
移動平均フィルタ少し話がそれてしまいますが、折角経時データを用意したので、XcosとSimulinkで各種フィルタを行う場合の使い勝手について、それぞれの比較をちょっとしてみます。
XcosXcosの場合、Sourceの中にあるRfile_fで、txtファイルの読み取り等を行うことができます。
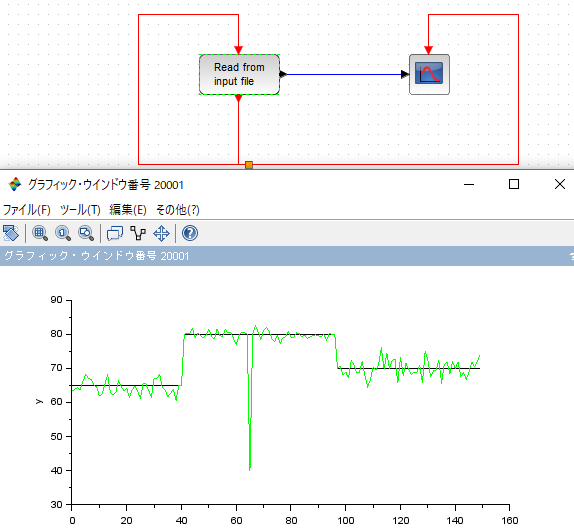
ただ、ここでちょっと厄介なのが、txtファイルをFortranフォーマットに整えておく必要があることです。様々な様式のデータを、前処理せずにXcosに流し込むことができないという点で使いにくさがあります。一方でSimulinkの場合は、前処理の必要がなく、そのままデータを流し込むことができるという点で非常に優れています。
SimulinkSimulinkの場合、CSV等をそのまま読み込むことができます。以下ヘッダー部分もそのまま読み込んで、表示してくれています。Xcosの際には、Fortranのフォーマットにするためにかなり時間がかかりましたが、Simulinkは一瞬で使い方を理解することができました。
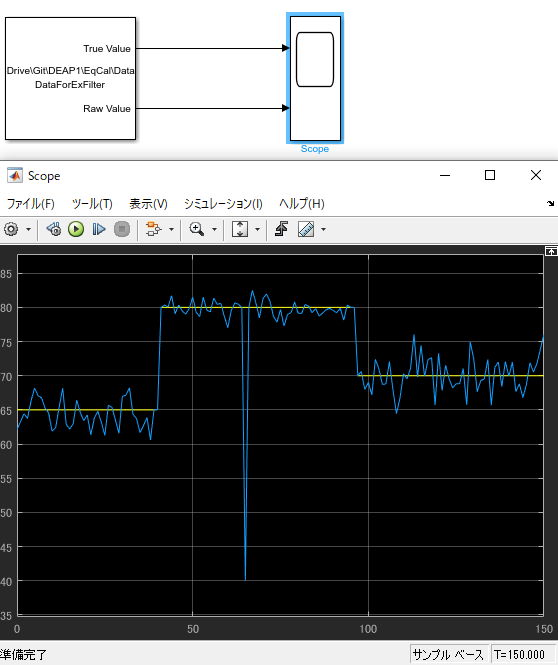
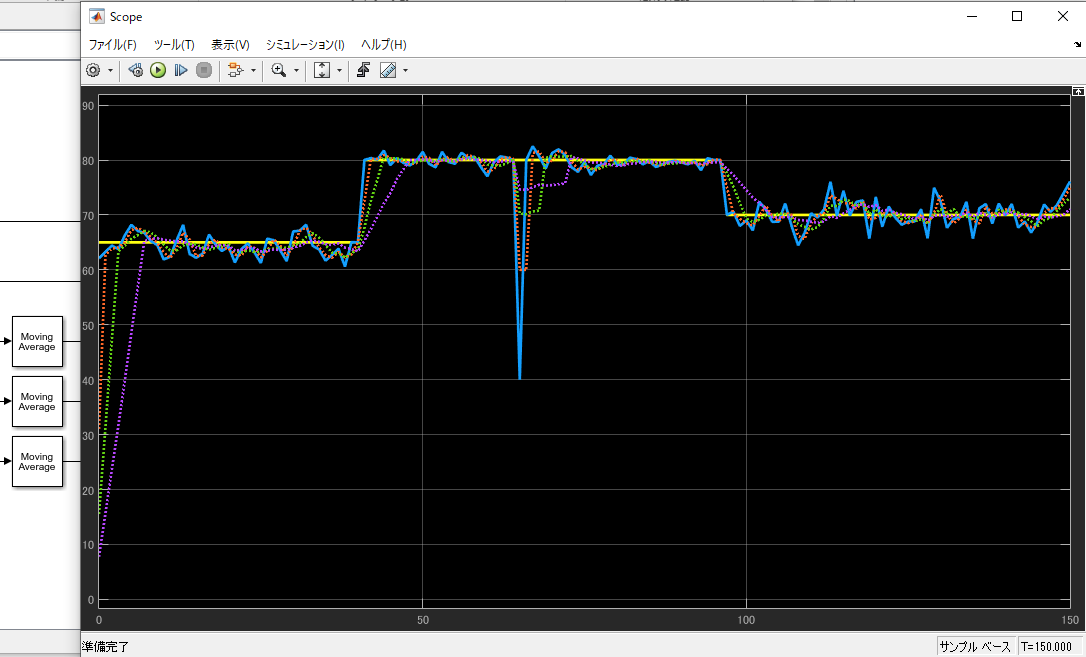
また、DSP System Toolboxを使うと、様々なフィルタを使うことが可能です。例えば、以下は上記ツールボックスのMovingAverageのWindowサイズをそれぞれ2、4、8とした場合の比較です。こうしたケーススタディが非常に容易かつ直感的にできる点がSimulinkの素晴らしい点です。Xcosも良いのですが、やはりSimulinkと比べるとツールボックスの充実度と使い勝手の観点で大きな差があります。
AVEVA社のAVEVA Process Simulation(旧SimCentral)を使って、Data Reconciliationを行う例をご紹介します。
AVEVA Process Simulationではサブモデルを、後付けでモデルに追加することが可能ですので、Transmitterモデルに対して生値とデータレコン後の値の誤差値を計算するモデルを、実機データがあるTransmitterに対して追加することで、簡単にData Reconciliationを行うことが可能です(ver5.2以降ではサブモデルを用いることなく、設定可能なモデルが搭載されています)。こちらでも紹介していますが、簡単な例を以下動画で示しています。
また、専用のSDKを用いることで、Pythonを介してOSI PIとの接続、シミュレーターとの接続を行うことが可能ですので、以下のようにプラントデータを元にData Reconciliationを行うことも可能です。
定常状態を前提としたData Reconciliationを行う場合、まず定常状態であることを判定する必要があります。ただ、プラントが完全にピタッと定常状態で保持されているということは期待できません。計器のホワイトノイズを上述のフィルリングである程度除いたとしても、マニュアルによる運転操作や原料の変動等によってプラントが過渡状態にある場合、ホールドアップでのデルタが生じているため、流量だけでバランス自体を取ることができません。このためData Reconciliationを行う前にプラントが定常状態であるかどうかを判断する必要があります。
以下仮想的に、一定の流量値50kg/hrに変動幅5kg/hr程度の標準偏差を持つ正規分布方の時系列データを2時間分程度作成、等分割し、両データの平均に対する有意差があるかを見てみます。
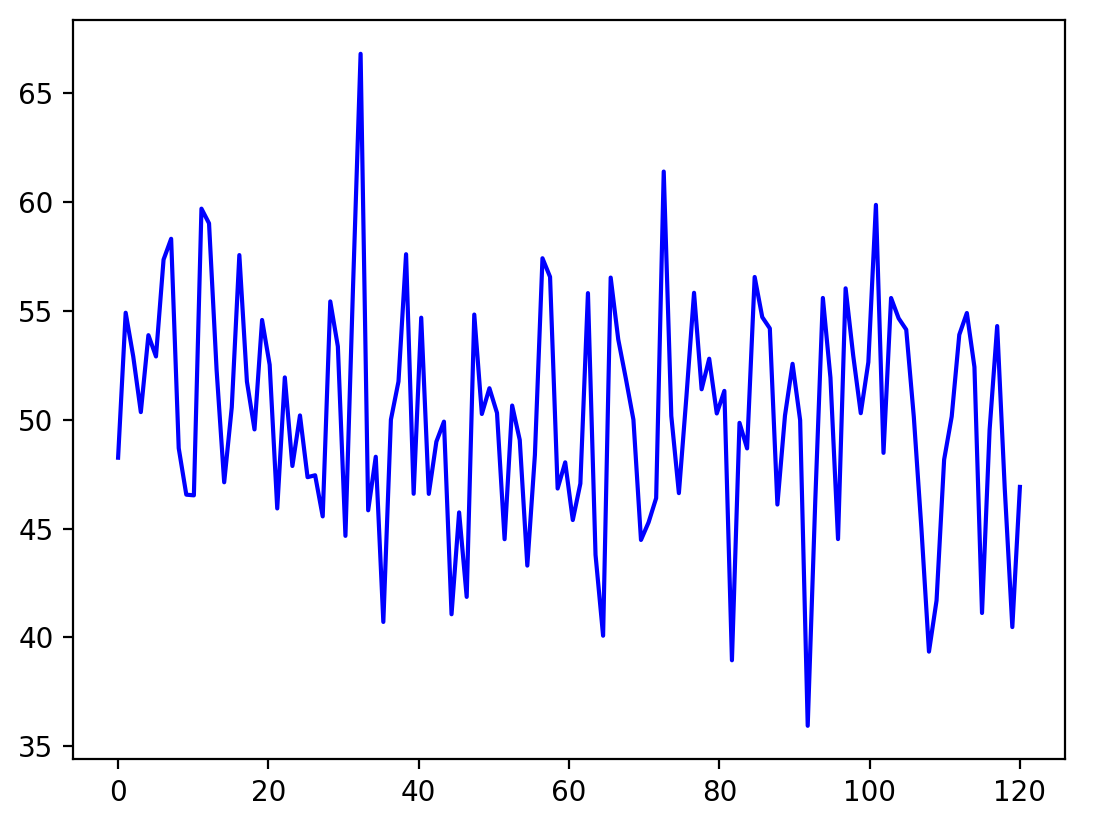
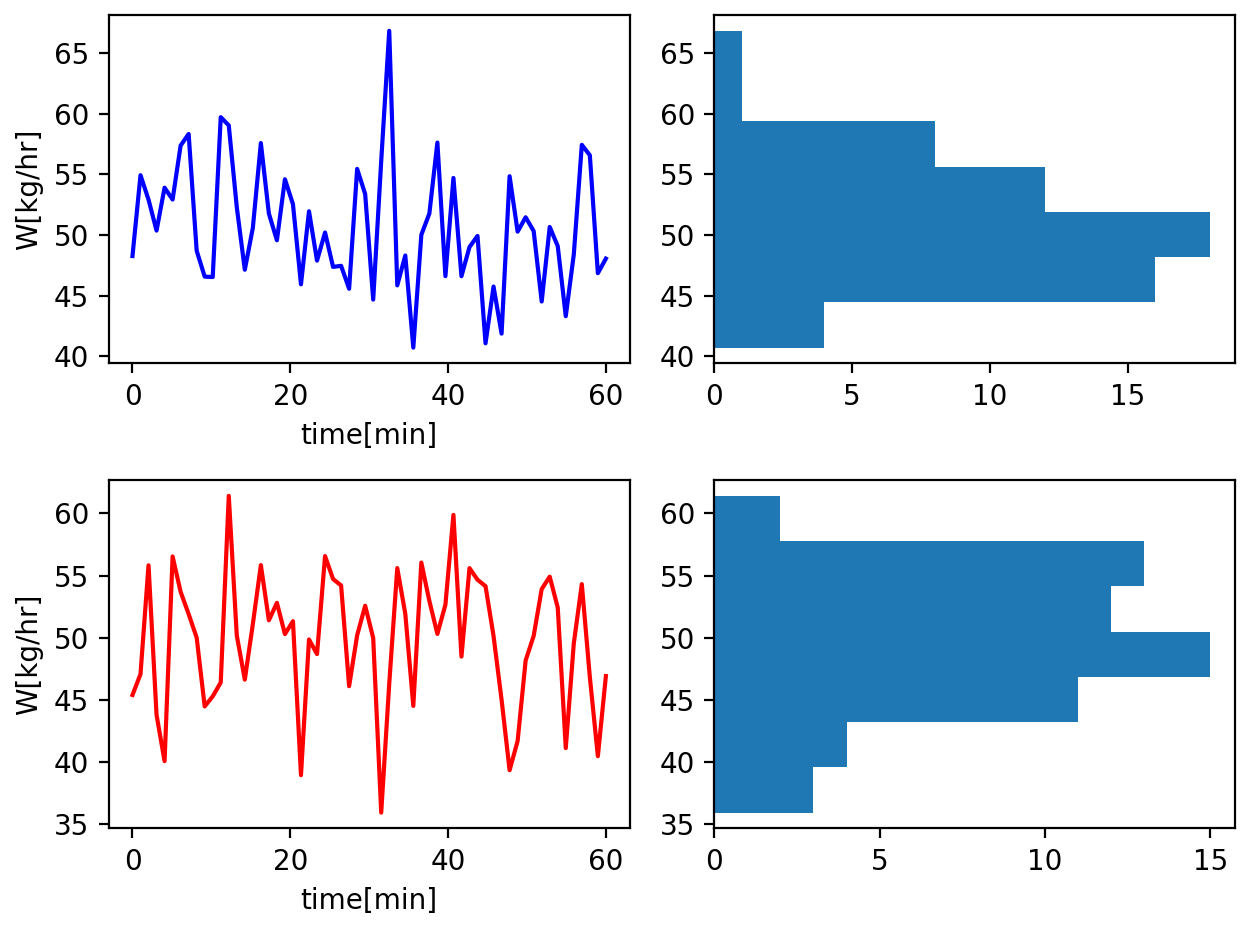
上述の両データは、F比:1.134、F検定95%:1.540となっているため、期待通り分散がほぼ等しいデータとして見ることができます。
分散が等しいとした場合のt検定を行うと、p値は0.398程度となっており、有意差は無いことが確認できます。
一方で、上述の後半のデータに対して、例えばRamp操作で0->10[kg/hr]分の流量を上乗せした以下のデータに対してt検定を行うと、p値は6.83e-5程度となり、明確な有意差を確認することができます。
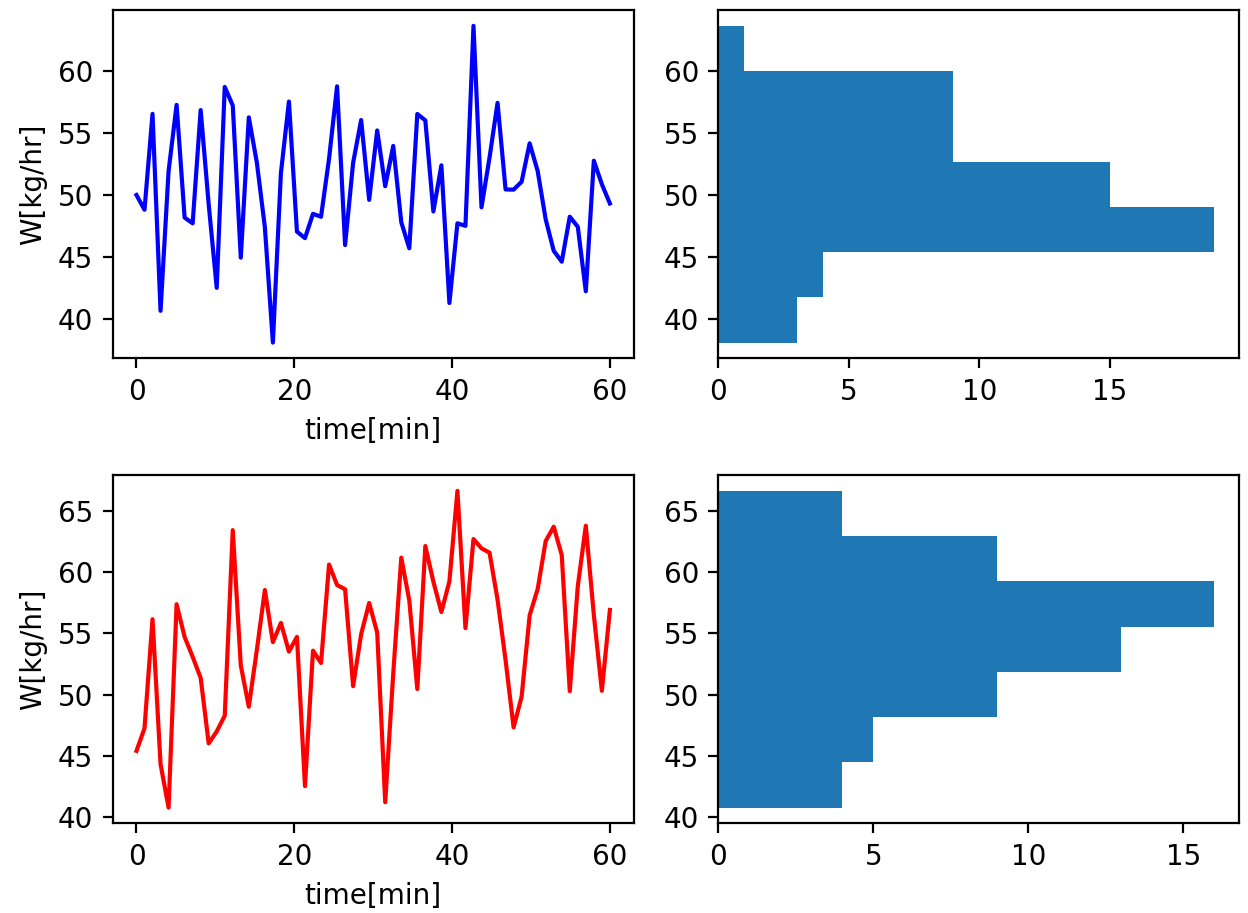
大まかな目安としての定常判定はできそうです。
非定常データに対するData Reconciliation
真の意味でのデジタルツインを行っていくためにはプラントのリアルタイムデータに対する非定常のData Reconciliationが必要になるかと思います。まだ答えは出ていませんが、非定常に対するデータリコンをするために考慮するべきポイントをまとめていきます。
プラントが常に定常状態であれば、上述のようにバランス制約から実機の流量計との整合性を計器誤差の範囲内で納められるかと思います。しかしながらくどいですが、実際にはプラントが定常状態であることはありませんので、特定の時刻の生値でそのままData Reconcilationをすることができません。
Dynamic Data Reconcilationに、非定常データに対するData Reconcilationの方法が記載されています。
ソフトセンサー
上述のデータリコンしリエーションを行い、整合性の取れた値を求められれば、シミュレーターの結果をソフトセンサーとして用いることができます。またここではシミュレーターを部分的に用いる、あるいはシミュレーターを全く用いないソフトセンサーの実装についてまとめていきます。
まずソフトセンサーの勉強に役立つお勧め書籍を以下ご紹介します。 Soft Sensors for Monitoring and Control of Industrial Processes, Luigi Fortuna (著), Salvatore Graziani (著), Alessandro Rizzo (著), Maria Gabriella Xibilia (著)
実プラントの生データは、ソフトセンサーに使う上で以下の問題点があります。
計器異常や非定常操作による外れ値、遅れや無駄時間、サンプリング時間等の時間的な差異、データの欠損値等は取り除く、あるいはモデルに組み込んでおく必要があります。
上記紹介書籍の第3、4章でデータの取り扱いについて記載されていますので、一部紹介します。
外れ値の検出
外れ値の検出については、3σルール、
データ補完
一般的なデータの補完方法について、ご紹介します。
お勧め書籍:Cによる理工学問題の解法、佐藤 次男 (著), 中村 理一郎 (著), 伊藤 惇 (著)
n個のデータ(x1,y1)~(xn,yn)について、以下3つの条件を満たす3次スプライン関数S(x)を考えます。(x1 < x2 < ... < xi < ... < xn)
①1次導関数S'(x)が連続であること : \(S'_i(x_{i-1})=S'_i(x_{i})\)
②2次導関数S''(x)が連続であること : \(S''_i(x_{i-1})=S''_i(x_{i})\)
③i=1~nに対し、S(xi)=yiであること
さらにNatural Cubic Splineの場合、境界条件として、S''(x)の始点と終点を0としますが、こちらは後述します。
まず条件②から考えていきます。(大概の解説はS(x)=\(ax^3+bx^2+cx+d\)から追いかけていきますが、私は上記お勧め書籍で説明されている2次導関数から追いかける方が分かりやすいので、②からスプライン関数を求めます。)
3次関数S(x)の2次導関数は、1次関数となります。
ここで、S''(x)=M(x)、i=1~nに対して、Mi=M(xi)とすると、前述の2次微分の連続性から、\(x_{i-1} \leqq x \leqq x_i\)において、下図のようにS''(x)を表現することができます。
S''(x)を積分し、S'(x)、S(x)を求めます。
S(x)が求まったので、続いて条件③を評価します。\(S(_{i-1})=y_{i-1}\)、\(S(_{i})=y_{i}\)より、以下積分定数C1、C2を求めます。
最後に、条件①を評価します。
S'(x)が連続であることから、\(x_i\)において、\(S'_i(x_i)\)と\(S'_{i+1}(x_i)\)は等しくなります。これを整理すると、
上式に前述のNatural Cubic Splineの始点と終点の境界条件である\(M_1=0, M_n=0\)を加え、\(M_1 ~ M_n\)が求まります。
上式の\(M_2 ~ M_{n-1}\)を求めるには、三重対角行列アルゴリズムであるトーマスアルゴリズム(TDMA)を用います。
以下具体的な解き方については、「Silverlightでツール作成」の項で後述いたしますが、Excelを使う場合は、逆行列が簡単に求まりますので、もっと簡単です。
scipyのモジュール:interpolate.CubicSplineを使うことでcubic splineの作成が可能です。
例として、次の6点を通るスプライン曲線を考えます。
(11.1,34.3),(20.9,62.1),(40.0,64.5),(65.6,75.9),(73.9,90.7),(90.9,95.9)
x1~x6、y1~y6を代入し、M2~M5を求めていきます。(natural cubic splineの条件から、M1=M6=0)
Excelの場合は、minverse関数で逆行列を、mmult関数で行列の積を簡単に求めることができます。
試しに元データの中間点のXの値からYの値を求めプロットすることで、以下のようにCubic Splineが求まります。(もっと刻みは増やした方が良いです)
簡単なサンプルツールをSilverlightで作成しましたので、こちらで最終形のイメージを掴んでください。(こちらがツールへのリンクになります。Internet exploreでご参照ください)
上図のサンプルツールは、プロット上をクリックすると、該当するポイントのX-Yデータを読み取り、生成した各X-Yデータ間をNatural Cubic Splineで繋ぎます。
ただし、新しくプロットする点:\(x_{i+1}\)は、\(x_i < x_{i+1} \)である必要がありますので、ご注意ください。
上記のツールではNatural Cubic Spline補完をするため、生成した各Xのデータを8等分し、そのXにおけるYを補完で求めています。
ツールの実装C#でも行列計算はMath.Net Numericsでも可能ですが、重くなるのでTDMAを入れ込みます。
なお、AVEVA Process Simulation(旧SimCentral)には、上述のようなカーブからデータ補完を自動で行う機能が搭載されており、ポンプの性能曲線等の画像データに合った性能表現が簡単に設定できるようになっています。
当サイトに不具合、ご意見等ございましたらCEsolutionにお知らせください。
