分離計算について
蒸留分離、吸脱着、膜分離の基本をまとめていきます。
・蒸留塔のHydraulic、Flooding、Weepingの経験式
・液液抽出
気液平衡計算の基本
理想溶液
・純成分の蒸気圧
純成分の蒸気圧は例えば、PerryのHandbook等で確認することができます。
PerryのHandbookでは蒸気圧は以下の式形(型)となっています。(単位:Pa)
$$ln(P)=C_1+C_2/T+C_3ln(T)+C_4 \cdot T^{C_5}$$また、DYNSIMやSimCentralといったシミュレーターをお使いの方は、それぞれ専用の物性確認インターフェイスがあります。モデルを作り始める前にまずは各物性の適用範囲や最適な物性モデルが選択されているか、必要なパラメーターが揃っているか等確認することをお勧めします。シミュレーターをお使いの場合は、各ソフトで物性の回帰機能等も付属しています。
・K値の推算
圧力、温度が一定にコントロールされている場合のフラッシュ計算を考えると、気液平衡の収束計算の流れは以下の通り
①平衡定数Kの初期値、Vapor fractionを適当に与え、各相の組成を仮決めします。平衡定数の初期値については、低圧のハイドロカーボンであればWilsonの相関式が適用できます。
②圧力、温度、組成から各相の圧縮係数zを算出(zの算出方法については、こちらを参照ください)
③zから各相、各成分のフガシティ係数を算出します。
④各相、各成分のフガシティ係数から平衡定数を算出します。
⑤④で求めた平衡定数を元に各相の組成を算出し、\( \sum y_i- \sum x_i \)が許容誤差以下になるまで平衡定数をアップデートし、収束計算を行います。
多成分系を例として、もう少し上記の収束条件について具体的に書きます。
基本式を順に整理していきます。フィード:F、ガス流量:G、液流量:Lとすると、定常状態における各成分、及び全体の入出収支は以下の形となります。
$$ L + V = F \tag{1.1}$$ $$x_i \cdot L + y_i \cdot V = z_i \cdot F \tag{1.2}$$また各成分の平衡定数を\(K_i\)とすると、液相、気相の各組成は以下の関係式が成り立ちます。
$$y_i = K_i \cdot x_i \tag{1.3}$$上記3式をまとめなおすと、以下の関係式が成り立ちます。
$$x_i \cdot L + K_i \cdot x_i \cdot V = z_i \cdot (V+L) \tag{1.4}$$(1.4)式を(1.1)式で整理しなおすと、
$$x_i = \frac{z_i} {(K_i-1)(V/F)+1} \tag{1.5}$$また、(1.5)式は(1.3)式から、
$$y_i = \frac{K_i \cdot z_i} {(K_i-1)(V/F)+1} \tag{1.5}$$ここで、\( \sum y_i - \sum x_i = \sum {(y_i- x_i)} \lt \epsilon \)が収束条件なので、以下が成り立つまで繰り返し計算を行います。
$$ \sum_i \frac{(K_i-1) \cdot z_i} {(K_i-1)(V/F)+1} \lt \epsilon \tag{1.6}$$Cf)上記収束条件について:McGraw-Hill chemical engineering series のSeparation Processesに詳細が記載されています。
収束計算の手法についても、記載されています。(Regula falsiとNewton法)
Cf)Wilsonの相関式
Wilson, G., ; “A modified Redlich-Kwong equation of state applicable to general physical data calculations;” 65th AIChE National meeting, Paper No15C, 1968
蒸留塔理論段数の算出
作成中
以下2成分系で、フィード流量:F[kg-mol/hr]、留出量:D[kg-mol/hr]、缶出量:B[kg-mol/hr]、成分1のフィード組成:zf、留出組成xD、缶出組成:xBとします。
カラム全体の全物質収支と、成分1の物質収支は
$$ F = D + W $$ $$ F \cdot z_F = D \cdot x_D + W \cdot x_W $$ 濃縮部の操作線(下図水色のライン)準備中
回収部の操作線(下図ピンク色のライン)準備中
操作線の交点操作線の交点はフィード流体の性状によって変化します。
Wolframのデモプロジェクトの中にMcCabe Theieleの図解法サンプルがあります。フィードのq値を変更させていくと、階段線図がどのように変化していくのか視覚的に確認できます。
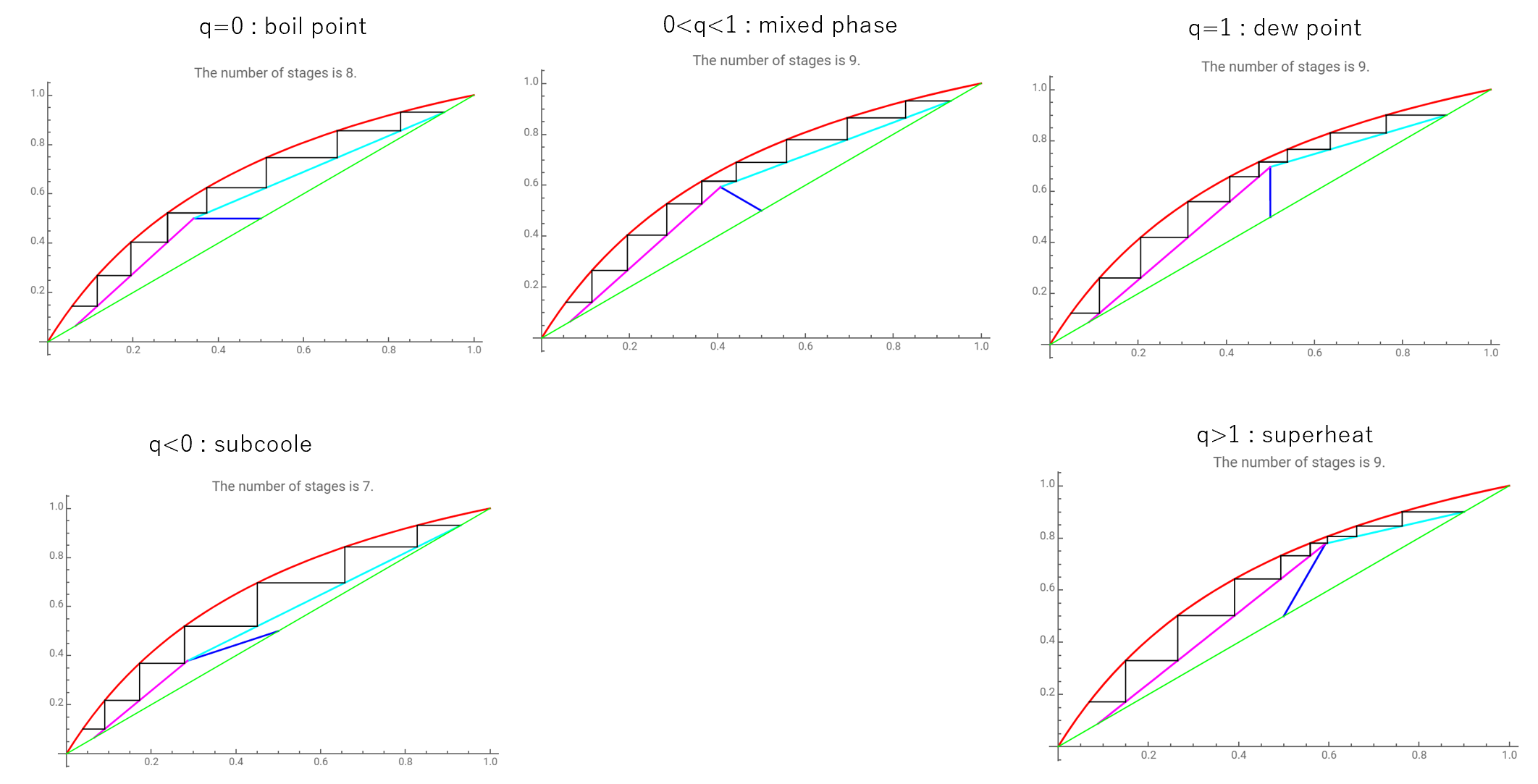
cf. WOLFRAM Demonstrations Projectを使用しています。
作成中
作成中
こちらの本が詳しいです。
蒸留塔のHydraulic、Flooding、Weepingの経験式
作成中
作成中
参考書籍
Kister, H. Z. “Distillation Design;” McGraw-Hill Book Company, Page.297
液液抽出
作成中
物質移動に基づく分離計算の基本
拡散係数の算出については、こちらにまとめています。
速度論型蒸留塔の基本
まずおすすめ書籍からです。
速度論型の蒸留塔モデルは式が煩雑になってくるため入口の敷居が高いですが、まず一冊読むとすれば、この本です。
具体的な例題を含めて紹介されており式の検証が行いやすい点と、計算のアルゴリズムも紹介されています。
特に8章Film Theoryでは、3成分系において、境界面での濃度差から具体的にどのように物質移動が起こるのか具体例を含めて説明されており、大変参考になります。
移動物質係数を求めるには、拡散係数の算出が必要となります。代表的な手法はこちらにまとめています。
作成中。
AVEVA社のPRO/IIのモデルを例にご紹介します。
吸脱着の基本
こちらの本が分かりやすくてお勧めです。
AVEVA社のSimCentralのモデルを例にご紹介します。以下はExapleに入っている工業用PSA装置のサンプルモデルになります。
サンプルは特定の成分、吸着材に対するデータのみのデータしか入っていませんが、吸着モデル自体がサブモデルとなっており、置き換えが可能となっています。
膜分離モデル
こちらの伊東先生のHPが大変参考になります。
以前、伊東先生のHPを参考にAVEVA社のDYNSIM(ソフトの内容に関してはソフトウェアベンダーにお問い合わせください。)を使って、CO2とCH4膜分離の簡易モデル作成を試みたことがあるので、以下簡単にご紹介します。
上記のHPで紹介されている膜分離モデルでは、供給側、透過側ともに完全混合状態とした場合の分離モデルが紹介されています。
DYNSIMに膜分離ユニットは残念ながらありませんが、Streamsetという非常に便利なユニットがあります。
ストリームユニットでは、所定の成分を、所定の流量流すことができるため、仮想の膜分離ユニット(Header)から、外部で計算した透過流量を強制的に排出させることで、簡易的な膜分離ユニットの表現ができます。
外部で計算させる場合は、Miscellaneousユニットと、Pointsユニットをよく使います。
Pointsユニットを使うと、ユーザーが任意の変数をフローシート上に作成することができます。以下の例では、圧縮係数や透過係数、カット比、膜面積、膜厚み等の変数をフローシート上に作成し、それらを使った計算式をMiscellaneousユニットで取り扱っています。(下図のMem1C、Mem2CがMiscellaneousユニット、P1、P2といったポイント付きの変数がPoints、Res1、Perm1といったユニットがStreamsetユニットになります。なお、Header内の温度や組成等の変数は直接Miscellaneousユニット中に参照させて計算させることが可能です)
DYNSIMではUAM(User Added Model)というユーザーのカスタムモデルをC++で作成することもできるのですが、こうしたちょっとした工夫でモデリングの幅が広がるのが面白いところです。
ただ上記のモデルでは両側とも完全混合と仮定しており、長手方向の圧力プロファイルを考慮しておりません。
(後述のAVEVA社のSimCentralが出てきた際に、この点は少し改良しました)
AVEVA社のSimCentralでは、モジュール単位のモデルを作成し、それらをN個接続させることが可能です。
作成中
COCOでは解析解を用いた膜分離モデルのサンプルが用意されています。
水-エタノール分離カラムの留出液に対して、エタノールの選択率と未透過側、透過側の流量比を入力し、未透過液をカラムに戻しています。
当サイトに不具合、ご意見等ございましたらCEsolutionにお知らせください。
