VBA
化学工学、数値計算に役立つTipsを紹介します。
まだコンテンツは少ないですが、今後状態方程式法の解法、常微分方程式の解法等、数値計算、制御のTipsを追加していく予定です。また、VBAを使わなくてもExcel関数とGoal SeakもしくはSolverの組み合わせでも実は結構いろんなことができます。Excelの活用方法についても少しまとめていければと考えています。(回帰計算や、MINVERSE、MMULTを組み合わせた連立方程式の解法等)
WMI(Windows Management Instrumentation)の活用
事前準備
・VBAを使いやすくするためのTips
私が初めてコードっぽいものを書いたのはVBAでした。(大学でCの授業はありましたがからきしダメでした)
しかし、なかなか上達せず何度か諦めかけましたが、以下の点を意識するようになってから、様々なコーディングが非常にやりやすくなりました。
・Debug.Printを使い、正常に値が格納されているか気になる箇所はイミディエイトウィンドウに表示する
・F8で1行ずつコードを進める
・ローカルウィンドウで各オブジェクトや変数の格納状況を確認する
・Option Explicitでの定数宣言
以下事前準備として上述の設定方法等少し詳しく整理します。
準備中
よく使う機能
・データ入力されている最終行、列の取得▼
例えばE3を起点に"最終行""を取得する場合
Range("E3").End(xlDown).Row もしくは Cells(3,5).End(xlDown).Row
例えばE3を起点に"最終行""を取得する場合
Range("F2").End(xlToRight).Column もしくは Cells(2,6).End(xlToRight).Column
使用例例えば以下のようなデータを一旦配列に格納したいという場合の設定について、以下一例を記載します。
コード例
Debug.Printで複数点抜き打ちで結果を確認するようにしています。
・Worksheet関数(回帰、逆行列、転置、複素数計算)▼
複素数計算私は都度書くのが面倒なので、よく使う関数はVBAで登録しています。
以下登録例▼| Complex(a,b) | 複素数の表現。a+bi |
|---|---|
| ImProduct(a,b) | 複素数同士の積。a*b(a、bはそれぞれComplex(x,y)の形で記載します) |
| ImDiv(a,b) | 複素数同士の割り算。a/b(a、bはそれぞれComplex(x,y)の形で記載します) |
| ImReal(a) | 実数部。x+yiのxを返します |
| Imaginary(a) | 虚数部。x+yiのyを返します |
| ImAbs(a) | 複素数の絶対値を返します。 |
| ImExp(a) | exp(x+yi)を求めます。無駄時間を掛け合わせる場合に使用します。 |
・名前定義セルの取得▼
Excelでは各セルに名前を定義することができます。
定義されたセルの名称でセルの値を呼び出すと、行や列の挿入でセルの位置が変わってしまっても良いので使い勝手が良いです。 (なによりCells(3,4)*Range("B4")等、セルの番地で記載しているとなんの計算をしているか分からないですが、分かりやすい名前をシート側でつけておけば式の意味も分かって混乱しません。)
例えば、Excelで1次遅れの計算を行う場合に、時間刻み、時定数を、それぞれdtFOL、τFOLと定義しておきます。 (左上のボックスにセルにつけたい名前を入力します。A3やB4等、セルの番地と被るような名前は入力できません)
これで、以下のように、VBA中でセルの番地を数えたり調べたりしなくても、名前で呼び出すことができますし、τやdtのセル番地が変わっても参照がズレてしまうことがありません。
・Solver、GoalSeakの呼び出し
ExcelのSolverやGoalSeakは回帰計算に便利な機能です。
VBAと組み合わせることで、様々な活用方法があります。
一例として、NRTLのbinary parameterを回帰計算で求める方法、1次遅れプロセスと実データのフィッティングを行う方法を以下ご紹介します。 (Solver、Goal Seakの基本的な使い方についてはこちらをご参照ください。)
・classの活用▼
VBAでもクラスを定義、利用することができます。
例えば私の場合、状態方程式の解を求める際に、クラスとして3次方程式の解法(Viete,Cardano)を登録しておき、呼び出す等の活用をしています。
以下の例では、SRK式(zの3次方程式):\(z^3-z^2+(A-B^2-B)-AB=0\)で、a=-1、b=\(A-B^2-B\)、c=-ABとして、3次方程式の解を求めるクラスにa、b、cを渡しています。
・For Each xx In yyの活用▼
準備中。
xmlファイルの読み込み
・名前空間付xmlファイルの読み込みについて
・Windows8.1のMSXMLについて
MSXML2.DOMDocumentは使えない→MSXML2.DOMDocument60にする必要がある。
以下リンクを参照しました。
MSXMLを使ったExcel VBAがWindows 8.1で動かない時の対処方法SQL接続
・SQL認証とWindows認証▼
DYNSIM ver5.3.2まではデータベースがSQLであったため、よくデータの抽出に活用していました。Excelを用いる場合は、Excel自体がデータベースになり得るので、あまりSQL接続の需要は無いかもしれませんが、簡単にご紹介します。
WMI(Windows Management Instrumentation)の活用
・ユーザー名を調べる▼
Excelでユーザー名やホスト名を調べたりする場合にWMIは役立ちます。
・特定の実行プログラムのパスを調べる▼
準備中
状態方程式の解法
・純成分のzの求め方▼
非線形方程式の解法について、現実的な問題を取り扱った方が面白いので、一例としてSRKのzをいくつかの手法で解いていきます。
・3次状態方程式の解法1~2分法▼
準備中
・3次状態方程式の解法2~はさみうち法▼
準備中
・3次状態方程式の解法3~Cardano法とViete法▼
準備中
活量係数型の解法
・NRTL
・2成分系のXY、PXY、γの出力を行いたい場合、例えば、以下のように各成分の蒸気圧、バイナリデータをエクセルの特定のセルに保存しておくことで簡単に求められます。
Excelの場合、データをいちいち探してこなくてもまとめてエクセルに保存しておけば良いのが、利点ですね。また、回帰を行いたい場合、Solverが使えるのも便利です。
設定準備中。
以下のように出力をグラフで整理します。
エクセルの方が手軽ですが、グラフ形を成形したりするにはPythonの方が断然楽ですので、個人的にはPythonの方がお勧めです。
常微分程式の解法
・陽解法▼
陽解法の考え方についてはこちらをご参照ください。
ここでは、VBAで陽解法を実装する方法を記載します。まず以下の簡単な一階微分から求めます。
$$\frac{dx}{dt}=x、x(0)=1$$離散化された以下の式をVBAで実装します
$$x_{i+1}=(1+\Delta t)x_i、x(0)=1$$コード例は以下になります。
準備中
続いて2階微分の場合です。以下の常微分方程式を陽解法で求めます。
$$\frac{d^2x}{dt^2}=-x、x(0)=0、\frac{dx}{dt}=1$$離散化された以下の式をVBAで実装します
\begin{align*} \begin{bmatrix} x_{i+1} & \\ u_{i+1} & \end{bmatrix} &= \begin{bmatrix} 1 & \Delta t \\ -\Delta t & 1 \end{bmatrix} \begin{bmatrix} x_i & \\ u_i & \end{bmatrix} \end{align*}コード例は以下になります。
準備中
・陰解法▼
陰解法の考え方についてはこちらをご参照ください。
ここでは、VBAで陰解法を実装する方法を記載します。まず以下の簡単な一階微分から求めます。
$$\frac{dx}{dt}=x、x(0)=1$$離散化された以下の式をVBAで実装します
$$x_{i+1}=\frac{x_i}{1-\Delta t}、x(0)=1$$コード例は以下になります。
準備中
続いて2階微分の場合です。以下の常微分方程式を陰解法で求めます。
$$\frac{d^2x}{dt^2}=-x、x(0)=0、\frac{dx}{dt}=1$$離散化された以下の式をVBAで実装します
\begin{align*} \begin{bmatrix} 1 & -\Delta t \\ \Delta t & 1 \end{bmatrix} \begin{bmatrix} x_{i+1} & \\ u_{i+1} & \end{bmatrix} &=\begin{bmatrix} x_i & \\ u_i & \end{bmatrix} \end{align*}・Runge-Kutta法▼
Runge-Kutta法の考え方についてはこちらをご参照ください。
ここでは、VBAでRunge-Kutta法を実装する方法を記載します。まず以下の簡単な一階微分から求めます。
$$\frac{dx}{dt}=x、x(0)=1$$以下、参考までにシンプルな2階微分方程式を陽解法と4次のRunge-Kuttaで解いた場合の収束状況を図示しています。
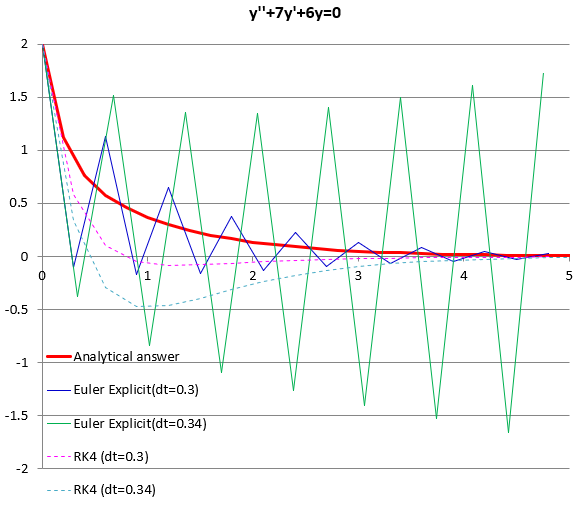
非定常モデルの表現
上述の常微分方程式の解法を用いれば、簡単な非定常計算モデルをExcel上で表現することができます。
以下、単純な流量コントロールモデルを表現する場合の例になります。
流量セットを1500[kg/hr]とし、差圧10[kPa]のSource、Sink間でIdeal型、Position typeのPIDで流量を徐々に上げています。シンプルなモデルですが、非定常計算の理解を深める第一歩として、私はSource→Valve→Sinkでのモデリングをお勧めします。
今はあまりExcelを使っていませんが、Excelの場合、全ての変数やパラメーターを画面上に置いておけるのが便利です。
オープンループの単位ステップ応答
・1次遅れプロセス▼
まず解析解から求めます。
遅れの時定数をτとすると、プロセス応答は以下の式となります。(詳細はこちら)
$$\frac{1}{1+\tau s}$$単位ステップ入力を与えると、伝達関数は以下で表されます。
$${F\left( s \right)}=\frac{1}{s(1+\tau s)}$$ $${F\left( s \right)}=\frac{1}{s}-\frac{1}{s+1/\tau}$$逆ラプラス変換をすると、
$${\mathfrak{L}^{ - 1}}\left\{ {F\left( s \right)} \right\} =f\left( t \right) =1-e^{-t/\tau}$$続いて陰解法で求めます。元の微分方程式(詳細はこちら)から、
$$\tau \frac{dy}{dt}+y=u$$上式を離散化して、
$$\tau \frac{y_n-y_{n-1}}{\Delta t}+y_n=u_n$$ $$y_n=\frac{u_n \Delta t + \tau y_{n-1}}{\tau+\Delta t}$$上述の離散化式と解析解を比較すると、以下のようになります。
dt=0.5sec、τ=5secの場合
dt=0.1sec、τ=5secの場合
VBAのコードは以下になります。
安定性評価
・Bode線図の作成▼
2次遅れ要素の例として、以下の伝達関数のBode線図を作成します。
$$G(s)=\frac{K}{s(s+1)}$$s=jωを代入すると、
$$G(j\omega)=\frac{K}{j\omega(j\omega+1)}$$VBAでは前述のように、複素数計算をWorksheet関数でそのまま行うことができます。
$$G(s)=\frac{K}{(s+1)(s+2)(s+3)}$$・Nyquist線図の作成▼
準備中
$$G(s)=\frac{K}{(s+1)(s+2)(s+3)}$$・安定性の判別法▼
1.フルビッツの安定判別法▼
以下の特性方程式に対して、各係数が存在し、かつ正であること、またフルビッツ行列式が全て正であることが、安定の必要十分条件となります。
$$a_0s^n+a_1s^{n-1}+...+a_{n-1}s+a_n$$フルビッツの行列式は以下の通り
$$\begin{eqnarray} H_i = \left| \begin{array}{ccccc} a_{ 1 } & a_{ 3 } & a_{ 5 } & \ldots & a_{ 2i-1 } \\ a_{ 0 } & a_{ 2 } & a_{ 4 } & \ldots & a_{ 2i-2 } \\ 0 & a_{ 1 } & a_{ 3 } & \ldots & a_{ 2i-3 } \\ 0 & a_{ 0 } & a_{ 2 } & \ldots & a_{ 2i-4 } \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \ldots & a_{ i } \end{array} \right| \end{eqnarray}$$2.ラウスの安定判別法▼
準備中
3.ナイキストの安定判別法▼
準備中
当サイトに不具合、ご意見等ございましたらCEsolutionにお知らせください。
