教科書的なPIDの形は以下の基本形になります。

設定値SP(t)と、測定値PV(t)の偏差E(t)=PV(t)-SP(t)とすると、制御出力MV(t)は、以下の式で表されます。

$$MV(t)=Kp\left[E(t)+\frac{1}{Ti}\int E(t) dt + Td \frac{dE(t)}{dt}\right]$$

上記の基本形：Ideal型の他にも以下Series型やPrallel型があります。

$$MV(t)=Kp\left[E(t)+\frac{1}{Ti}\int E(t) dt \right] \left[ 1+ Td \frac{dE(t)}{dt}\right]$$ $$MV(t)=KpE(t)+\frac{1}{Ti}\int E(t) dt + Td \frac{dE(t)}{dt}$$

AVEVA社のDYNSIMではいずれの形式のアルゴリズムも選択することが可能です。

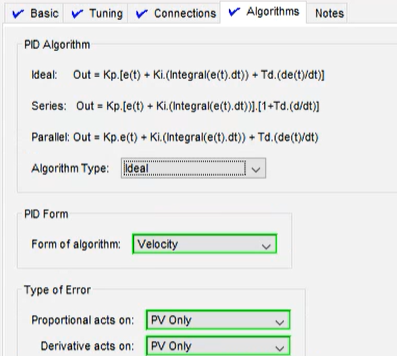
AlgorithmsタブのAlgorithm Typeから変更が可能です。

少し特殊なアルゴリズムとしてLegacyというタイプも用意されています。こちらはIdealと似ていますが微分項が少し特殊な形をしており、速度型、位置型の選択もできないため私は殆ど使ったことがありません。（デフォルトがなぜLegacyなんだろうというのが疑問です、、）

上記のPIDの基本形は連続時間における表現となっておりますが、実際にはDCSのスキャンタイムは通常0.5sec程度で固定されていますので、実際の制御を模擬する場合には上式を離散化する必要があります。

スキャンタイムをΔtとすると、位置型は以下のようになります。

$$MV(t_n)=Kp\left[E(t_n)+\frac{1}{Ti} \displaystyle \sum_{i=0}^{n}E(t_n) \Delta t + Td \frac{\Delta E(t_n)}{\Delta t}\right]$$ $$ \Delta E(t_n) = E(t_n)-E(t_{n-1})$$

速度型は以下のようになります。

$$ \Delta MV(t_n)=Kp\left[ \Delta E(t_n)+\frac{1}{Ti} E(t_n) \Delta t + Td \frac{\Delta (\Delta E(t_n))}{\Delta t}\right]$$ $$ \Delta E(t_n) = E(t_n)-E(t_{n-1})$$ $$ \Delta (\Delta E(t_n)) = (E(t_n)-E(t_{n-1}))-(E(t_{n-1})-E(t_{n-2}))$$

速度型は、前回の出力値に対して、現在時間における修正分ΔMVを足し合わせて出力値を求めます。

このため、Manual⇒Autoへの切り替え時にも大きなバンプを抑えることができます。

逆に位置型は、PV値が流量計のようにノイズを含みやすい場合に、安定的に制御することができます。（特に、後述のI-PD型の場合）

※参考書籍

Instrument Engineers' Handbook, Volume One: Process Measurement and Analysis (English Edition)

AVEVA社のDYNSIMではいずれの形式のアルゴリズムも選択することが可能です。

少し分かりにくいですが、AlgorithmsタブのPID Formから変更が可能です。

前述の基本形（PID型）に加え、以下の２つの制御方法があります。（位置型で記載しています）

I-PD型（比例微分先行型）

$$MV(t_n)=Kp\left[PV(t_n)+\frac{1}{Ti} \displaystyle \sum_{i=0}^{n}E(t_n) \Delta t + Td \frac{\Delta PV(t_n)}{\Delta t}\right]$$ $$ \Delta PV(t_n) = PV(t_n)-PV(t_{n-1})$$

PI-D型（微分先行型）

$$MV(t_n)=Kp\left[E(t_n)+\frac{1}{Ti} \displaystyle \sum_{i=0}^{n}E(t_n) \Delta t + Td \frac{\Delta PV(t_n)}{\Delta t}\right]$$ $$ \Delta PV(t_n) = PV(t_n)-PV(t_{n-1})$$

比例微分先行型は、目標値変更によるキックを抑制することができ、またオーバーシュートを小さくすることもできますが、目標値変更に対する追従性が遅いという問題があります。

カスケード制御における２次ループのように、設定値変更に対する追従性を良くしたい場合は、微分先行型を採用した方が良いことになります。

AVEVA社のDYNSIMではいずれの形式のアルゴリズムも選択することが可能です。

少し分かりにくいですが、AlgorithmsタブのType of Errorから変更が可能です。

PID制御を行う際、操作端の上下限値を超えた入力を受けた場合、実際の操作量は上下限に張り付いた状態となってしまい、PIDの出力値と実際の操作量に差異が生じます。

この状態が継続すると、目標値との差分が積分項によって蓄積されていってしまい、大きなオーバーシュートを発生させてしまいます。

こうした状況、ワインドアップを避けるためにいくつか対応方法がありますが、例えばAVEVA社のSimCentralに搭載されているアンチ・リセット・ワインドアップをご紹介します。

以下のビデオは、SimCentralで意図的に液面制御が十分に動作できないようにバルブ条件を厳しく設定し、フィードを急変させることで液面制御がワインドアップを起こす状況を作成しています。

画面上側がデフォルトのPIDコントローラー、下側が意図的に積分のアンチ・リセット・ワインドアップの動作を止めた場合になります。

両者のトレンドを比較していただくと、アンチ・リセット・ワインドアップが効いていない下側のケースでは、積分値が積み上がり、正常な制御レンジに戻るまでにかかる時間が長くなっていることが分かります。

後述の２自由度制御とも重なりますが、PIDは理想的には①「設定値の変更に対して素早く追従すること」に加え、②「外乱が入ってきた際にも素早く制定できること」が望ましいです

上記の２つの目的を１つの制御で実現することは難しいですが、特定の外乱に対して、制御すべき方向がある程度事前に予測できる場合は、フィードフォワードとフィードバックを組み合わせることで制御性能を向上させることができます。

こちらの本に記載されているFigure6.4[Feedback trim for flow-to-flow control of the hot water process]を参考に、以前AVEVA社のDYNSIMを使って作成したモデルを以下参考のために示します。

上記の例は冷却水をスチームで加温し温水を作るプロセスにおいて、冷却水の流量や温度が変化した場合に必要となるスチーム量を計算し、フィードフォワードで先行して制御に加算する形としています。

トレンドグラフを見ていただくと、フィードバックのみ（FB only）の場合に比べ、フィードフォワード＋フィードバック（FF + FB）の方が温水の温度変動を抑制できていることが確認できます。

なお、上図ではフィードバック制御のみの時と、フィードフォワード＋フィードバック制御の切り替えをボタンで行っていますが、DYNSIMではこのようにボタンによって特定のイベントを起こすことが可能になっています。（シナリオという機能もあり、スクリプト形式でイベントを書き下すこともできますが、GUI上から操作できるという点でボタンを使った方が便利なケースもあります。後述のシーケンスの項目もご参照ください）

検出端と操作バルブが離れており、大きな無駄時間があるような系に対して、通常のPID制御だけでコントロールをかけてしまうと、PID出力の結果が反映されるまでの間の誤差も累積されてしまい、ハンチングが生じてしまいます。

こうしたケースでは、一定の周期で制御とサンプリングを繰り返すサンプルPID制御が有効です。

以下はAVEVA社の非定常シミュレーターDYNSIMを用いた簡易検証モデルです。強制的に長い無駄時間を設けた熱量調整モデルですが、サンプルPID制御を行っていないNorPIDと比べて、制御時間2秒、サンプリング時間20秒としたサンプルPIDの方が安定的に制御できていることが確認できます。

PIDは、理想的には①「設定値の変更に対して素早く追従すること」に加え、②「外乱が入ってきた際にも素早く制定できること」が望ましいです。

①、②を１自由度で同時に満たすことはできないため、１自由度で制御する場合はどちらかを犠牲にする形になります。

2自由度制御では、外乱の影響の抑制、設定値への追従性を共に

ラプラス変換は微分方程式を解く際にも役立ちますが、なにより制御の構成を視覚的に捉えるのに役立ちます。

初めは抵抗感があるかもしれませんが、まずは最低限以下だけ知っておくと良いかと思います。

また１次遅れプロセスの伝達関数の項を見ていただくとラプラス変換の有難みが少し体感いただけるかと思います。

関数f(t)のラプラス変換

$$\mathfrak{L}\left[ f( t) \right] = \int_0^\infty [f( t ){e^{ - st}}dt]$$

原関数(original function) f(t)のラプラス変換

$$\mathfrak{L}\left[ f( t) \right] = F( s )$$

像関数(image function) F(s)の逆ラプラス変換

$$\mathfrak{L}^-1\left[ F( s) \right] = f( t )$$

１次遅れプロセスの例として、Perry Handbook8版の8章を参照に以下記載します。

A成分が一定流量F[m3/sec]、濃度\(C_{in}\)[kg-mol/m3]で反応器に入り、反応速度定数k[1/sec]でB成分に変化する反応を考えます。

ある時間における反応器内のA成分の濃度を$C_A$[kg-mol/m3]とすると、物質収支は以下となります。

$$V\frac{dC_A}{dt}=FC_{in}-FC_A-kVC_A$$

液相反応でボリュームは非圧縮性、反応速度定数は一定（F,V,k一定）とすると、両辺をF+kVで割り、

$$\frac{V}{F+kV}\frac{dC_A}{dt}=\frac{F}{F+kV}C_{in}-C_A$$

V/(F+kV)をτ、F/(F+kV)をKとすると、上式は以下となります。

$$\tau\frac{dC_A}{dt}=KC_{in}-C_A$$

上式でτが時定数、Kがプロセスゲインとなります。

時定数τ、プロセスゲインKの1次遅れプロセスの伝達関数は以下となります。

$$G(s)=\frac{K}{\tau s +1}$$

1次応答プロセスに対するインパルス応答、ステップ応答は以下となります。

インパルス応答 $$f(t)=\mathcal{L^{-1}}\left[G(s)U(s)\right]$$

U(s)=1なので、

$$f(t)=\frac{K}{\tau}\mathcal{L^{-1}}\left[\frac{1}{s+1/ \tau}\right]=\frac{K}{\tau}e^{-t/\tau}$$ ステップ応答 $$f(t)=\mathcal{L^{-1}}[G(s)U(s)]$$

U(s)=1/sなので、

$$f(t)=K\mathcal{L^{-1}}\left[\frac{1}{s \cdot (\tau s+1)}\right]=K\mathcal{L^{-1}}\left[\frac{1}{s}-\frac{1} {s +1/ \tau}\right]$$ $$f(t)=K(1-e^{-t/\tau})$$

逆ラプラス変換については、こちらのサイトが非常に丁寧で分かりやすいです。

限界感度法は無駄時間L/時定数Tが1より小さい範囲で適用します。

無駄時間が支配的なプロセスや、セットポイントのトラッキングテスト等では有効な効果が得られません。また、そもそも実プラントでこのようなテストはできませんが、例えばこちらのページでご紹介したように、シミュレーター上であれば限界発振するまでゲインを上げてパラメーターを求めるといったことも可能です。

限界感度法参照テーブル

	Kp	Ti	Td
P	0.5Kc	-	-
PI	0.45Kc	Pu/1.2	-
PID	0.6Kc	0.5Pu	Pu/8

過渡応答法参照テーブル

	Kp	Ti	Td
P	1/RL	-	-
PI	0.9/RL	L/0.3	-
PID	1.2/RL	2L	0.5L

IMC法参照テーブル（１次遅れ系）

	Kp	Ti	Td
PI	(Tp+L/2)/Kp(F+L/2)	Tp+L/2	-
PID	(Tp+L/2)/Kp(F+L/2)	Tp+L/2	(Tp・L/2)/(Tp+L/2)

Bode線図の基本をまとめていきます。

以下のシンプルな伝達関数を例として、Bode線図の作成方法をご紹介します。

$$G(s)=\frac{1}{5s+1}$$

上式に\(s=\omega j \)を代入します。

$$G(\omega j)=\frac{1}{5\omega j+1}$$

実数部:G(Re)と虚数部:G(Im)を求めます。

$$G(Re)=\frac{1}{25\omega^2+1}$$ $$G(Im)=\frac{-5\omega j}{25\omega^2+1}$$

ゲイン、位相を求めます。

$$Gain=20 \cdot log10 |G(j\omega)|$$ $$Phase=tan^{-1} \left(\frac{G(Im)}{G(Re)} \right)$$

Nyquist線図の基本をまとめていきます。

Matlab、Scilab、Excelを使ったBode線図、Nyquist線図の作成方法をまとめていきます。

・Bode線図作成ツール

Bode線図の作成ツールをsilverlightで作成したのでご紹介します。(Internet Explorerからのみで閲覧可能です)

伝達関数、計算条件を下図のように設定します。（2017/6/4現在、1次遅れのみの実装です）

Bode線図が確認できます。

各データの出力結果がテーブル形式で確認できます

閉ループのBode線図、Nyquist線図も実装しました。（2017/6/4現在Impulse応答のみ対応しています）

以下Matalbとの比較になります。

・ExcelでのNyquist線図、Bode線図の作成方法

作成方法：準備中

例として以下の伝達関数の各線図を紹介します。

$$\frac{K}{(s+1)(s+2)(s+3)}$$

Bode線図

Nyquist線図

・ScilabでのNyquist線図（重ね書き）、Bode線図の作成方法

・MatlabでのBode線図，Nyquist線図の作成方法

transfer functionの作成 : tf(Numerator,Denominator)

ex)tf([0, 1],[5 1])

Bode線図の作成：bode(transfer function)

ex)bode(tf([0 1],[5 1]))

Nyquist線図の作成：nyquist(transfer function)

ex)nyquist(tf([0 1],[5 1]))

システム同定に関しては、足立先生の本が素晴らしいです。

MatlabのSystemIdentification toolboxが無くてもシステム同定の基礎が分かるようにという配慮で改定された本著ですが、取っつきにくい制御の話を、分かりやすい言葉で書かれていますし、システム同定だけではなく、制御全般について網羅的に触れられているお勧めの本です。足立先生の著書は大好きなのですが、カルマンフィルタの本も素晴らしいです。

・予測誤差法（Prediction Error Method）

・ARXモデル（Auto-Regressive with extra input model）

・Matlab：System Indentification Toolboxの活用

こちらにDYNSIMのデータを使った例を紹介しています。

実プラントデータをお持ちの方は、是非実データでお試しください。

AND, OR, NAND, NOR

AVEVA社のDYNSIMで、各ロジックの動作イメージを以下動画でご紹介します。

こちらの動画で各ロジックの動作がイメージできるかと思います。

LATCH

LATCHはAND/ORユニットと比べると直感的に把握しにくいかもしれませんが、Advanced Digital Design with the Verilog HDLが非常に分かりやすいです。