個人的にPythonが有難いのは以下の点です。

①行列計算や多次元配列の取扱いが簡単

②複素数計算も可能（Bode線図やNyquist線図を作る際に便利）

③グラフ描画が容易で、綺麗な図が簡単に書ける

④外部ファイルとの入出力が行いやすい。(csv、txtは勿論、xmlやJSON等なんでも取り扱いやすい)

⑤変数の型宣言をしないでサクサク書ける（この書き方はプログラミング専門の方から言わせれば問題外だと思いますが、、）

⑥COM接続、OPC接続、OSI PIとの接続等、様々な外部リンクが簡単に行える

⑦最適化計算や非線形方程式、常微分方程式のソルバー、実験計画法、機械学習までモジュールが充実している。中にはcontrolライブラリやピンチ解析用のライブラリまであります。

⑧Jupyternotebookを使うことで、技術情報とコードの出力結果をまとめた資料作成が可能

Pythonでの数値計算の恩恵を受けるためにいくつか便利なライブラリを以下に紹介します。

・SciPy、NumPy、matpoltlib、scikit-learn：最適化計算や逆行列演算、グラフ描画等に便利です。

・PySide：GUIの作成に使えます。

・Streamlit：ウェブアプリ作成に役立ちます。

ちなみに私はインストールで何度もはじかれて苦戦しました。

インストールについてはゆくゆく整理していきたいと思います。

※2016.05.08追記：Scipy、Numpy、Matplotlibのインストールについては、こちらがよくまとまっています。

配列（array）、転置（transpose）、積(.dot)

※Numpyのインストールが必要です。

例えば以下の行列の表現は、x=np.array([[a,b,c],[d,e,f],[g,h,i]])となります。

$$x=\begin{bmatrix} a & b & c\\\ d & e & f \\\ g & h & i \end{bmatrix}$$

例えば以下の行列の表現は、a=np.array([[1],[2],[3]])となります。

$$a=\begin{bmatrix} 1 \\\ 2 \\\ 3 \end{bmatrix}$$

また上記の行列を転置した以下の行列はa=np.transpose(a)のように書けます。

$$a=\begin{bmatrix} 1 & 2 & 3 \end{bmatrix}$$

行列同士の積は、例えば行列aと行列bの積であれば、a.dot(b)と書くだけです。

例えば上記のシンプルな行列\(a=\begin{bmatrix} 1 & 2 & 3 \end{bmatrix}\)と、その転置行列の積をPythonで計算する場合、非常に短いコードで済みます。

コード例 　　 　　 　　 　　出力例

このようにNumpyを使うと、転置行列の作成、行列の積が簡単にできます。

固有値、固有ベクトル

linalg.eig()を使うことで、固有値、固有ベクトルを計算させることができます。

csvファイルの読み込み

numpyのloadtxtを使うと簡単に読み込むことができます。

import numpy as np
a = np.loadtxt("sampledata.csv",delimiter=",")

numpyのloadtxtを使うと簡単に読み込むことができます。

csvファイルを読み込んで、データの統計処理を行うのも簡単です。

最大値

print(np.amax(a))

最小値

print(np.amin(a))

算術平均

print(np.mean(a))

中央値

print(np.median(a))

標準偏差

print(np.std(a))

分散

print(np.var(a))

Excelファイルの読み込みについて

numpyのloadtxtを使うと簡単に読み込むことができます。

a = np.loadtxt("sampledata.csv",delimiter=",")

その他役立つ関数

乱数シードの固定

np.random.seed(N)

0.0~1.0の疑似乱数生成

以下、Nに生成したい乱数の数を入力します。

a = np.random.rand(N)

min~maxの疑似乱数生成

a = np.random.unifor(min, max)

標準正規分布に従った乱数生成

以下、locに平均値、scaleに標準偏差、sizeに生成する乱数の数を入力します。

a = np.random.normal(loc, scale, size)

累積和

以下の場合、出力は[1 3 6 10 15]となります。

a = np.array([1,2,3,4,5])
print(np.cumsum(a))

scipy.optimeze

curve_fit()、leastsq()等、回帰計算に役立つ関数が入っています。

非線形方程式の解法にはfsolveも有用です。

例えば以下は、複数の成分について気相のエンタルピーをleastsq()で特定の温度範囲におけるエンタルピーをAVEVA Process Simulationの17式から1式に回帰しなおした結果の一覧になります。

回帰結果の誤差が大きい場合はワーニングを出すようにしていますが、plotも合わせて表示していくと大きな誤差が出ていないかをパッと確認することができます。

for i in range(CN):
    obj_H = []
    obj_H0 = []
    dfhlatpara = []
    for j in range(len(T)):
        obj_H.append(eq17(hcorrar[i, :], T[j]))
    obj_H0 = lambda beta: obj_H - eq1(beta, T)
    betaID = leastsq(obj_H0, init_H, )
    coeff = pd.Series(betaID[0], index=["H1", "H2", "H3", "H4"])
    dfhlatpara = dfhlatpara.append(coeff)
    res = (obj_H - eq1(betaID[0], T)) / obj_H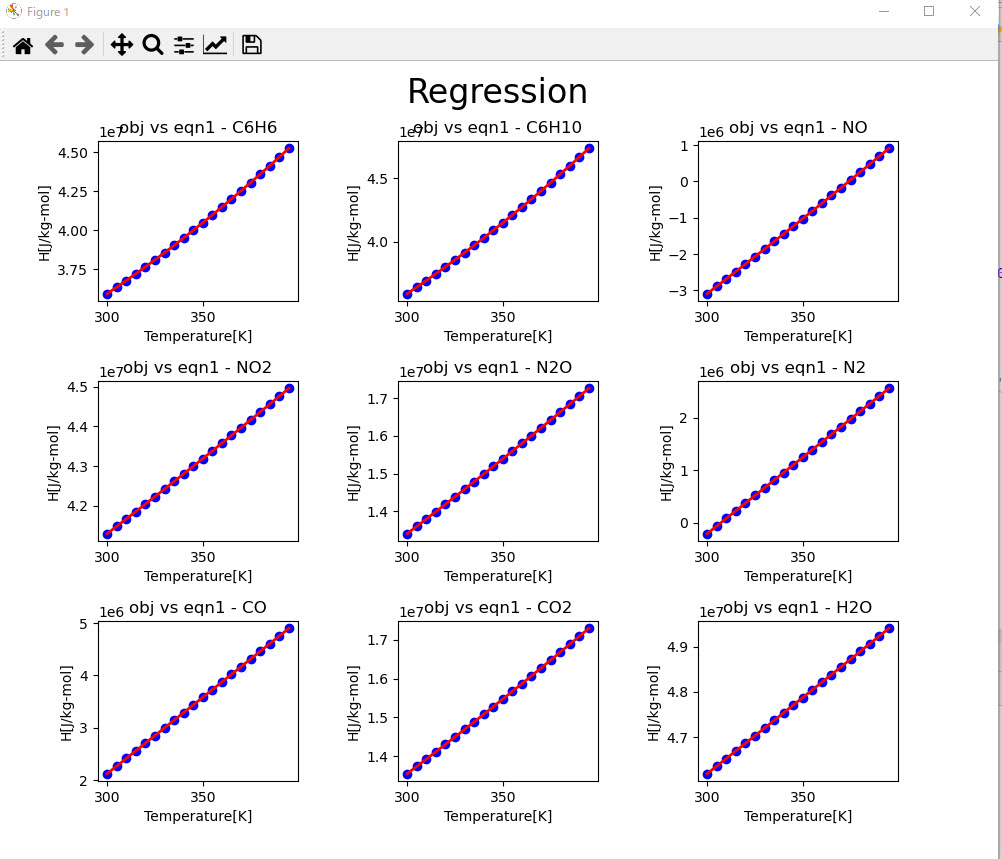

scipy.integrate

odeint()で簡単に微分方程式を記載することができます。（以下は例えば初期濃度Ca0、反応速度関数をfncとした亜場合の表現になります。）

Ca = odeint(fnc, Ca0, t)

ode()を使うと、set_integrator()で数値解法を変更することが可能です。

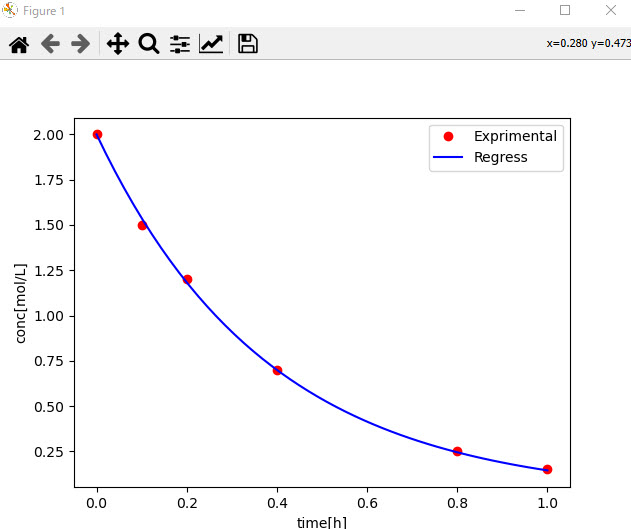
例えば、濃度に対する1次反応データに対して、反応速度定数を回帰したい場合、濃度の時間変化を以下のようにodeint()で表しておけば、この時間変化に対する回帰をcurve_fit関数で求めるといといったことも簡単に行えます。

使い勝手の良い関数をいくつかご紹介します。

read_csv(ファイルの置き場所,encoding)

csvファイルの読み込み

dropna()

欠損値の取り扱いに便利です。欠損値を含む(how=any)、あるいは全ての値(how=all)が欠損値である行、あるいは列(axis=1)を除外することができます。逆に欠損値を埋める場合はfillna()を使うことができます。

unique()

ユニークな値を持ったリストを作成することができます。

2dplot出力

詳細はゆくゆくまとめていきたいと思いますが、matplotlibのplotはsubplotをまとめて一つの形式で出力できるため、非常に便利です。

例えば、NRTLで水-EthanolのXY、PXY、活量係数をまとめてプロットしたいという場合、以下のようにまとめて表示させることが可能です。

以下のように各subplotの配置位置を2dgridで記載し、各suubplotの詳細を記載していきます。

3dplot出力

Qiitaのブログに詳細記載しましたのでご参照ください。

例として、以下のように理想気体と実在気体のPVT図を重ね書きする方法をまとめています。時間のあつ時にもう少し詳細に書きたいと思います。

三角座標のプロット

ブログに詳細記載しましたのでご参照ください。

seabornの役立つ関数

公式ページのGalleryに参考となる例が載っています。

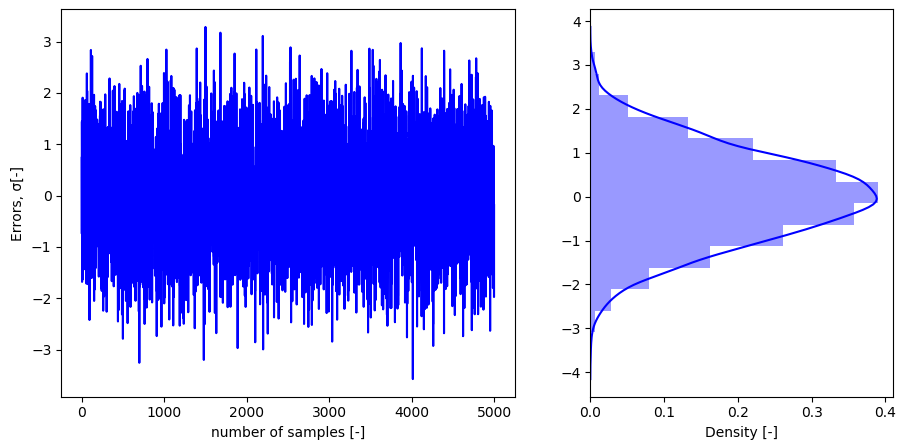
特にこちらのページに記載されているdistplot関数はヒストグラムに対してフィッティングを表示することもできて便利です。

以下は標準正規分布に従う乱数を生成し、そのヒストグラムとガウス確率密度関数への近似をオンにしたグラフを並べて表示した例になります。

scikit-learnの中には優れたモジュールが多数あります。いくつか手軽に使えるものを以下ご紹介します。

Opticsを使ったクラスタリング

異常予知を行う際、様々な手法がありますが、一つの手法として正常データのクラスターを作成し、最も近いクラスターと現在の運転データを比較、異常の有無判定を行う方法があります。

以下では、プラントの各ロードにおけるデータを、クラスタリングでザっと仕分けます。（製品流量あるいはフィード条件で条件を絞ればエクセルでも一瞬でできる作業ではありますが、ここでは少し身近な題材での検討をとしてテストしています）

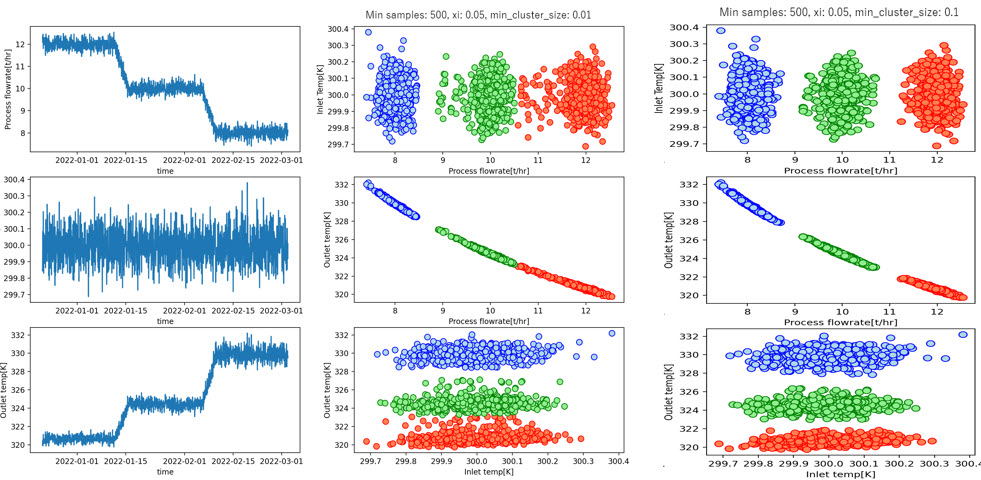
まずあまり意味のあるデータではありませんが、シンプルな熱交換器モデルに対して以下のような条件を与え、検証用のデータを作成します。

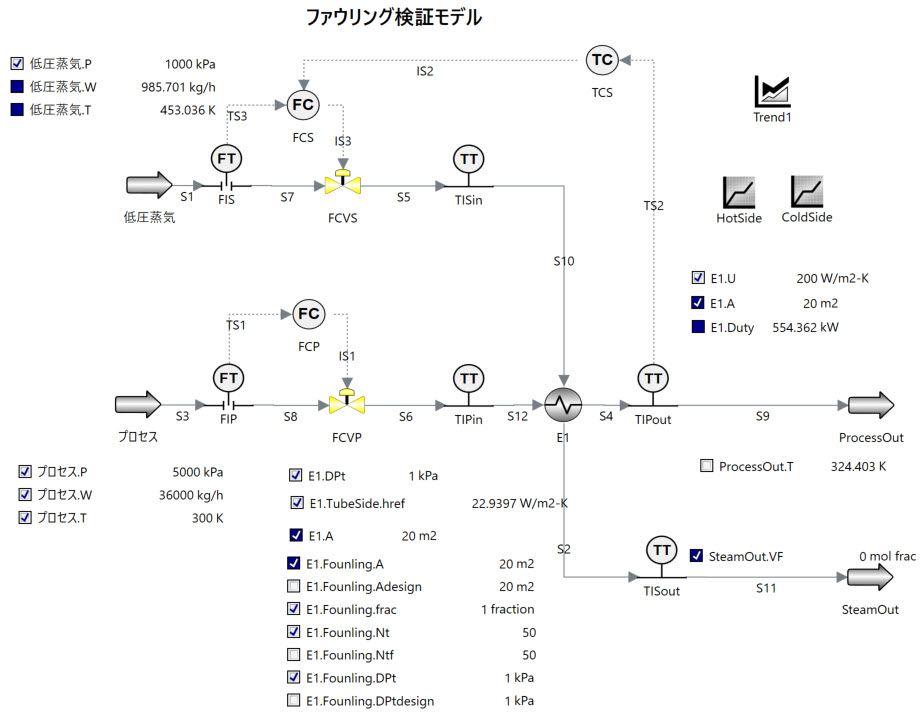
プロセス側のフィード流量、温度にホワイトノイズを追加し、ロードを100%から80%までリニアに落としていきます。この際用いる蒸気は低圧蒸気とし、こちらは飽和蒸気で常に必要流量を供給、また出口条件として完全凝縮して出ていくものとします。各Transmitterの測定精度は温度計、流量計共にそれなりの数値を入れています。

上記の計算条件で計算して生成したデータが左下のトレンドデータになります。これに対して、Opticsを適用して、各パラメーターを振ってみると、右下のトレンドではロード変更中のデータをある程度上手く弾いたクラスターになっているのが確認できます。

2021/1/23現在、以下個人的なメモ書き程度です。なぜわざわざこんなことを書いているかと言いますと私自身まだよく理解しておらず参考にはしない方が良いためです、、。

Pystanの基本的な使い方

公式ページの例題を見ると、設定方法が分かります。

基本的な流れとしては、Stanの書式に従って、data、parameters、modelをpystan.StanModelに与えてやります。

data、parameters、modelに与える情報はそれぞれ

ベイズの定理の基本

参考書籍としては、Bayesian Data Analysisがおすすめです。ベイズの定理の基本的な考え方について、血友病の遺伝に関する例とスペルミスの単語に対してどのように解釈するかといった例が紹介されています。ベイズの定理の紹介では大体袋の中に入った玉の数の例が取り上げられるケースが多いですが、現実的なテーマで興味深いです。ちなみに血友病に関しては、こちらのリンクも参考になります。

事後分布 \( p(\theta | y) \)は、事前分布\( p(\theta)\)、尤度関数\( p(y | \theta)\)、規格化定数f(y)を用いて以下で表せます。

$$ p(\theta | y) = \frac{p(\theta, y)}{p(y)} = \frac{p(\theta)p(y | \theta)}{p(y)} $$

PRO/IIとの接続

こちらでも触れていますが、PRO/IIはCOM接続が可能ですので、Pythonのwin32comを用いることで、簡単に接続できるようになっています。

PRO/II自体にもケーススタディ機能はついていますが、何千、何万というオーダーのケーススタディを行うには入力が大変ですので、データの読み込み、上書きを自動化することで省力化できます。

DYNSIMとの接続

こちらでも触れていますが、DYNSIMはOPC接続が可能ですので、PythonをOPC clientとすることで、簡単に接続できるようになっています。

また、少しハードルはあがりますが、専用の接続ブリッジを用いる方法もあります。

専用SDKを使ったAVEVA Process Simulation(旧SimCentral)との接続

こちらでも触れていますが、AVEVA Process SimulationはPythonとの接続が簡単に行えるようになっています。

データの読み込み、上書きだけではなく、Optimizerやシナリオ操作もPythonから行うことが可能です。

例えば、以下のようにPythonから熱交換器のネットワークを変更し、変更前後のコスト比較を行うといった操作も自動化することが可能です。

例えば、以下のVapor pressureのデータ（データはperryのhandbook参照）をテキストファイルに保存しておき、各係数を必要に応じて読みだすことを考えます。

$$ln(P)=C1+C2/T+C3ln(T)+C4T^{C5}$$

C1:73.649、C2:-7,258.2、C3:−7.3037、C4:4.1653E−06、C5：2

ただし、圧力の単位はPa、適用温度範囲は、273.16～647.096[K]となっています。

上述のC1～C5パラメーターを各行毎に区切ってテキストに入力しておけば以下のような形で読み込むことができます。

①f=open('VPwat.txt')で同階層にあるVPwat.txtを開き、

②lines2=f.readlines()でテキストファイルを１行ずつlines2に格納していきます。

※readlines()以外にも、read()、readline()があります。使い分けは以下のリンクが分かりやすいので、ご参照ください。

read()

①f.close()でテキストファイルを閉じます。

④他の蒸気圧推算法でも対応できるように、VPの係数はMax7個まで格納できるようにしています。この際、Cに格納するデータが空だとエラーが出るため、空の部分には0を代入しています。

⑤C1～C7までデータを格納していきます。この際、リストからそのままデータを引っ張ってくると改行コードが邪魔であるのと、数値として認識されなかったため、.strip()で改行コードを除き、float()でそれぞれを数値化しています。

このように、係数は分離して別置きしておけば、推算式が変わっても呼び出し元の関数を使い分けるだけで対応することができます。

Excelファイルの読み取り

まずxlrdを読み込みます。

import xlrd

例えば、物性データを「PhysicalData.xlsx」として保存し、ここから必要な情報を読み取る場合、以下のように設定します。

Excelデータ

Pythonコード

簡単に各行のコードをご紹介します。

Excelファイルの読み込み

book = xlrd.open_workbook('PhysicalData.xlsx')

シートの読み込み（index(0)がsheet1）

sh1 = book.sheet_by_index(0)

セルの値の読み込み（例えば、sheet1のB2セルの値の読み取り）

sh1.cell(2, 2).value

純成分のzの求め方

3次状態方程式の解法1～２分法

3次状態方程式の解法２～はさみうち法

3次状態方程式の解法３～Cardano法とViete法

こちらのリンクを参照にしました。

上記のリンクによると、odeinitを使うと、硬い問題かどうかによって、採用手法を自動で切り替えてくれるとのこと。

odeを使うと、解法を自由に選択できるようなので、まずはodeを試してみます。

主要な解法を以下に記載します。

BDFの呼出し：ode(function).set_integrator('vode', method='bdf')

adamsの呼出し：ode(function).set_integrator('vode', method='adams')

lsodaの呼出し：ode(function).set_integrator('lsoda')

ode45の呼出し：ode(function).set_integrator('dopri5')

(functionの部分に関数定義します。）

例題として、stiffな問題の方が差異が確認しやすいので、Van Der Pol方程式で各手法を比較してみます。

比較前提

Time step:0.1[sec]、積分時間：2000[sec]、μ:1000

van der pol方程式は以下の通り。

$$\frac{d^2x}{dt^2}-\mu \left(1-x^2\right)\frac{dx}{dt}+x=0$$

Adamsは今回の条件では解くことがでなかったため、その他の計算手法の計算速度を比較してみると以下のようになります。

BDF：19.71[sec]、lsoda：0.14[sec]、ODE45：13.73

続いてodeintを試してみます。

odeint(function, X0, t)の形で定義します。（X0が初期値、tが時間定義になります）

計算時間わずか0.0164[sec]。

基本的にはまずodeintを使うという戦略は妥当そうです。

なお、上記VDPの解をmatplotlibで作図すると以下のようになります（BDF）。

モジュールを使わずに陽解法▼ モジュールを使わずにRunge-Kutta法▼

Python-Control

Pythonには制御検討用のモジュールが用意されていますので、こちらを使うと簡単に制御モデルの表現が可能です。

こちらでマニュアルを確認することができます。

control.matlabを使うとMatlab風に記載することができます。

　プロセス伝達関数 　

ステップ応答を見たい場合は、step()を使うことができます。

　

例えば、確認したいプロセスの伝達関数が1/(s^2+7s+10)で表せる場合、以下のように事前に伝達関数を定義し、それをstep関数に入れることで表現できます。

num = [0, 0, 1]
den = [1, 7, 10]
s = tf(num, den)
y, t = step(s, T=arange(0, 3, 0.1))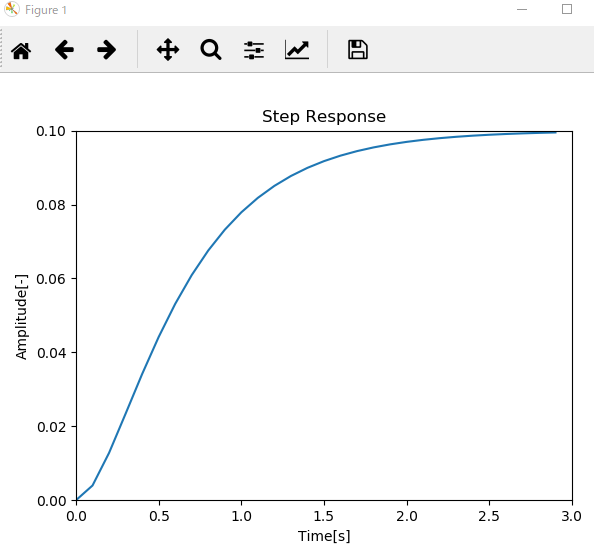

Bode線図の作成

Python-Controlを使うとBode線図の作成も容易にできます。

前節でご紹介した伝達関数sに対してBode線図を作成する場合は、以下のように１行のコードで済みます。

bode(s)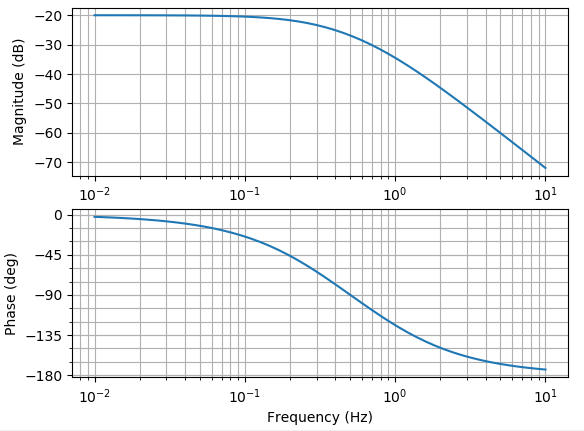

Nyquist線図の作成

Python-Controlを使うとBode線図同様、Nyquist線図も１行のコードで作成できます。

nyquist(s)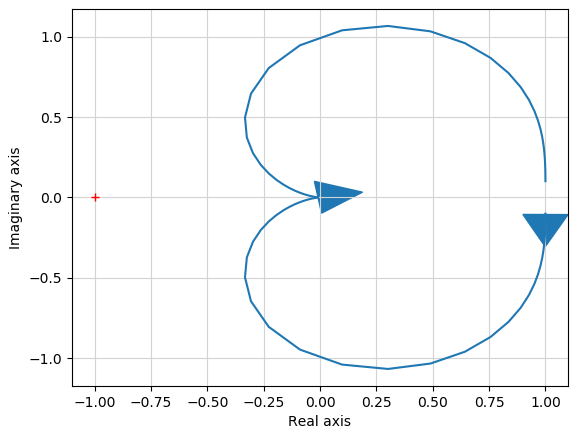

ただし、上記の伝達関数は1/(s^2+s+1)に対して書いたものです。

単一ページのHello Worldから、簡単な入力フォームを含むウェブアプリの作成方法をご紹介します。

単一ページのHello Worldから、csvファイルのアップロード、グラフ作成方法等ご紹介します。

Streamlitを使ったWebアプリの作成方法をご紹介します。

こちらのページに、簡単な説明を追加しました。

Pythonの学習に役立った講座、本をまとめていきます。

Udemyで参考になった講座

Udemyでは、ダントツで酒井さんの講座がお勧めです。話し方も分かりやすく、中身も充実しています。

Courseraで参考になった講座

データの可視化にはData Visualization wiht Pythonがおすすめです。

Applied Machine Learning in Pythonがお勧めです。最終課題がちょっと大変でしたが、、

Pythonの勉強を始めた頃、息子用に遊びで作ったコードです。意味は無いですが、対話型コードの参考として見てみてください。

While，If文の用法も確認でき、意外とこうした遊び感覚で作るプログラムの方が勉強になったりします。

※1 Shellでの入力要求はinput()の形で書きますが、そのままでは文字列として認識されてしまいます。

このため、数値として使用するためには、int(input())として一旦数値に変換する必要があります。

逆にprintで出力するには、文字列に変換する必要があるため、str()を使用します。