非定常シミュレーション
非定常シミュレーションの基本的な考え方、またDYNSIMの個人的に重要と思うTipsを少し紹介します。
非定常シミュレーションと定常シミュレーションを比較した場合、大きくは以下のような点が異なってきます。
・Flow-Driven⇒Pressure-Driven ・ホールドアップの考慮 ・時間変化の考慮 ・プロセス制御の考慮詳細は各項で触れていきますが、非定常シミュレーションに必要となる情報量が各段に増えてきます。
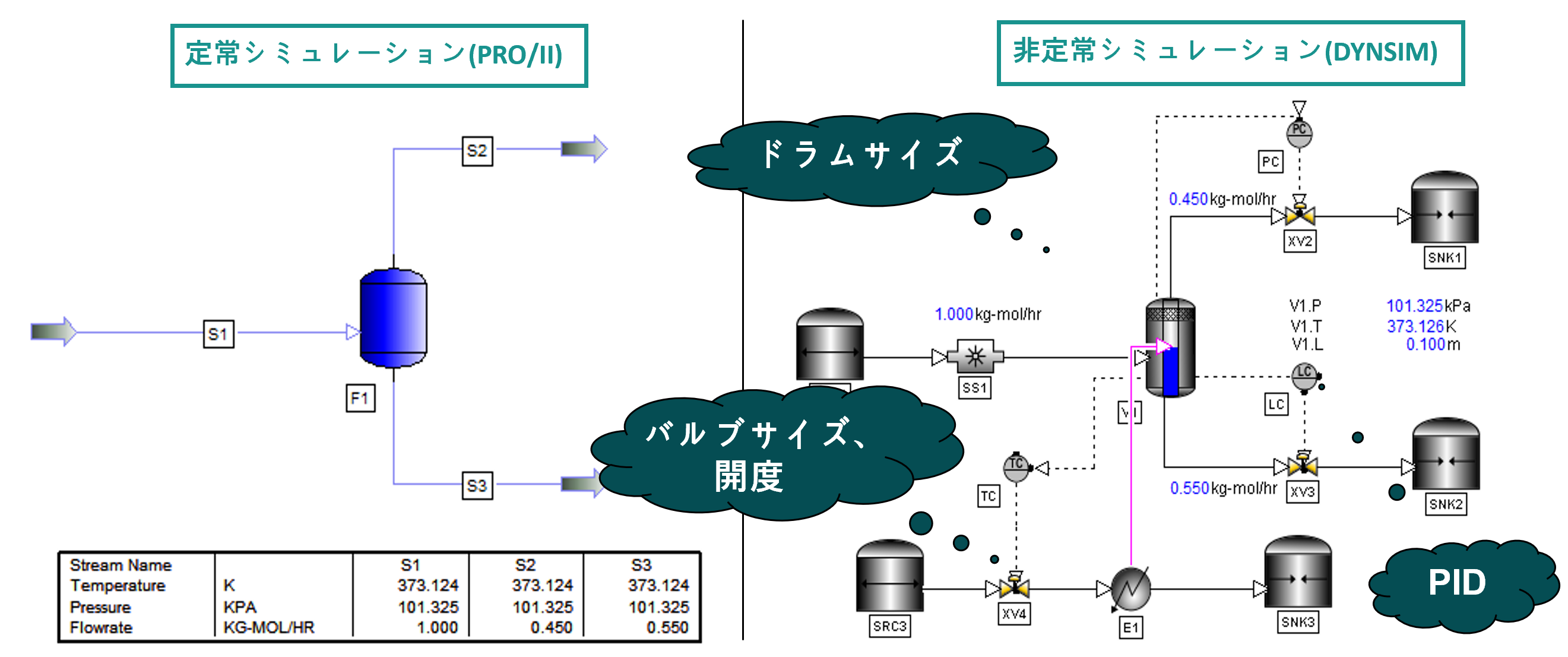
下図はそれぞれ定常シミュレーターPRO/IIと非定常シミュレーターDYNSIMで同じ状態を表現しようとした場合の差異のイメージになります。
左側に記載した定常シミュレーションの世界では、指定した流量、温度、圧力、組成を断熱でフラッシュさせるだけの単純なモデルですが、右側に記載した非定常シミュレーションで同様の定常状態を作ろうとした場合は、流量、圧力、温度、液面制御や、バルブやドラムのGeometry等、入力項目が各段に代わることが見てとれるかと思います。
 。
。
実プラントのトラブルシューティングにおいては、非定常シミュレーションが役立つ場面は多々ありますが、上記のようなモデリングの手間が非定常シミュレーションを行う上での大きな障害となり敬遠されがちです。
また、実プラントを正確に表現しようとすると、細かい配管まで全部入れ込もうとして途中でいざ走らせようとした際に、収束が難しく計算が破綻してしまったり、計算が重すぎて使い物にならなかったりするケースもあります。
検討目的に応じたポイントを掴み、計算速度、計算安定性、計算精度のバランスを見ながらモデル構築を行っていくことが重要になります。以下の項では、非定常シミュレーションを行う上で重要なポイントについて整理していきます。
時々刻々と変わるプラント内の動きを再現したい場合、非定常シミュレーションを行う必要がありますが、非定常シミュレーターには大きく分けて2種類の分類があります。
1つはプロセスシミュレーターを用いる集中定数系、もう1つは流動解析ソフト(CFD)を用いる分布定数系です。
集中定数系のシミュレーションでは、タンク内の空間分布や偏流等は考慮せず、完全に混合され一つのノードとして考えられるような場合に用いられます。
流動解析ソフト(CFD)では逆に空間分布を考慮することが可能です。例えば触媒槽内の偏流や配管内エルボ部での圧力変化を見たり、タンク内のスロッシング解析を行ったりという、単一ユニット内でも空間内分布が重要になるようなケースでは流動解析ソフトを用いた検討が必要となります。
大型プラント全体を丸ごとモデリングするようなケースではいくら計算能力が上がった現代とは言え、とても流動解析を行うことはできませんので、モデリングしたい粒度に応じてツールの使い分けが必要となります。
こちらで紹介しているように、一部を流動解析で求めてプロセスシミュレーションと繋ぐという使い方もされています。
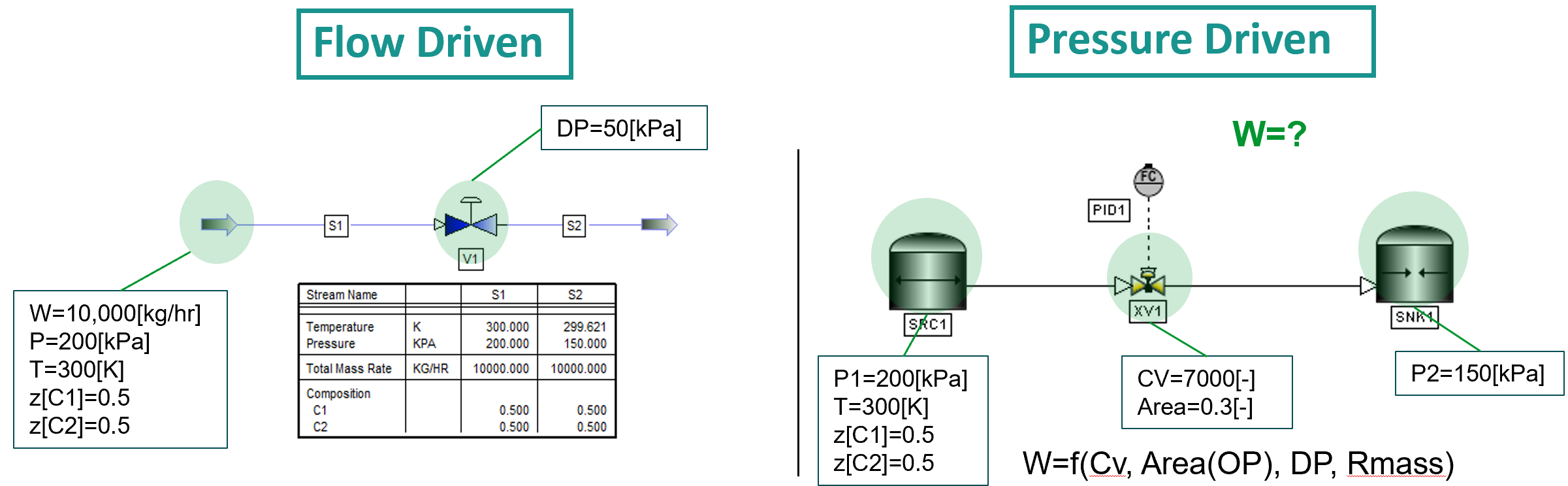
流量を境界条件とし、圧力を成り行きとする考え方をFlow-Driven、圧力を境界条件とし、流量を成り行きとする考え方をPressure-Drivenと言います。
前出の図で言うと、定常シミュレーションの場合では、通常流量とバルブの圧力損失を指定して、下流の圧力は成り行きとするFlow-Drivenの考え方になります。
一方で、非定常シミュレーションの場合は、上下流の圧力を指定して、流量が成り行きとなるPressure-Drivenの考え方に基づいています。(非定常シミュレーションでも例えば制限オリフィス等で流量が固定できる場合や、定量ポンプの下流からモデリングする場合等は、流量を境界条件とすることもありますが、基本的には圧力を境界条件、流量を成り行きとします。)
下図はそれぞれ定常シミュレーターPRO/IIと非定常シミュレーターDYNSIMで同じ状態を表現しようとした場合の差異のイメージになりますが、上記の説明と合わせてみていただくとイメージが湧きやすいかと思います。
 。
。
定常シミュレーションにおいては、常にユニットの入出の物質収支、熱収支が維持された状態となりますが、非定常シミュレーションにおいては入出がバランスせず、差異分が蓄積項となります。
逆流や反応項を除くと、以下のように記載できます。(物質収支は成分数の配列になります)
$$ \frac{dM}{dt} = In.F \cdot In.z - Out.F \cdot Out.z $$ $$ \frac{dE}{dt} = In.F \cdot In.H - Out.F \cdot Out.H $$ここで、M:各成分毎のホールドアップ[kmol]、F:モル流量[kmol/s]、z:モル組成[mol fraction]、E:内部エネルギー[kJ]、H:エンタルピー[kJ/kmol]
上記の蓄積項が、系内の圧力変動や組成変化の時間遅れに効いてくる形になりますが、急激な変化となるか、鈍ました変化となるかは容器のサイズ情報によるため、非定常シミュレーションにおいてはホールドアップ(Geometry情報の入力)が重要な因子となります。
特に内部流体が気体の場合は、正確な容量を入力していないと、実機とかけ離れた圧力ピークを示したり(容量が小さすぎる)、あるいは逆に全く圧力が変化しない(容量が大きすぎる)といった問題が起こります。
また、シミュレーターによっては、内部流体が非圧縮性流体か、あるいは圧縮性流体かによって式を切り替えるケースがあります。(AVEVA社のDYNSIMの場合は、Solution Optionタブ内で設定が可能です)
非定常シミュレーターにおいては、通常ヘッドも圧力バランス計算に組み込まれていますので、液面を正確に表現するためにも容器の形状入力が重要になります。(また液ノズルがボトムではなく側面にある場合は、ノズル位置も重要な情報となります)
また忘れ勝ちなのが熱容量の情報です。金属比熱、密度等の情報はシミュレーターによってデフォルトで想定している金属があるため、場合によっては見直しが必要となるケースがあります。
特に、系内の物質量の少ない高新空圧条件においては、わずかな外部雰囲気との熱の授受が思わぬ温度変動、ひいてはモデルの不安定さに繋がるケースもあるので、機器の熱容量に関する条件も確認が必要です。
時間変化を考えるには微分方程式を解いていく必要があります。
微分方程式の解法についてはこちらにまとめていますが、解法によって特徴が異なるため、検討用途に応じた選択が重要になります。
水撃計算等、非常に短い時間で変動するプロセス検討においては、時間刻みや配管のセグメント数によっては誤った解法を選択してしまうと、変動が増幅されてしまう、あるいは早期に収束してしまうといった問題があります。
AVEVA社のSimCentralでは、複数のソルバーが用意されていますが、水撃計算においてはtrapezoidalを用いることが推奨されています。理由については常微分方程式のページをご参照ください。
制御の基本については、こちらにまとめておりますので、ご参照ください。特にPIDのアルゴリズムについては、理解しておいた方が良いかと思います。また、PIDのチューングパラメーターについては、こちらの本が素晴らしいです。
PID制御を行う際、非定常シミュレーターにおけるPIDの演算周期は注意しておく必要があるポイントの一つになります。計算の時間刻みと演算周期が同期されており、実際の演算周期と大きく異なっている場合、条件によっては制御が効きすぎてしまうことがありますので、注意が必要です。
以下は、後述の計算条件で、径1m、高さ2mの円柱形のドラムにおける液面制御について、演算周期と計算刻みを一致させた場合と、単独で演算周期を入力した場合の比較になりますが、挙動が大きく異なっていることが確認できます。
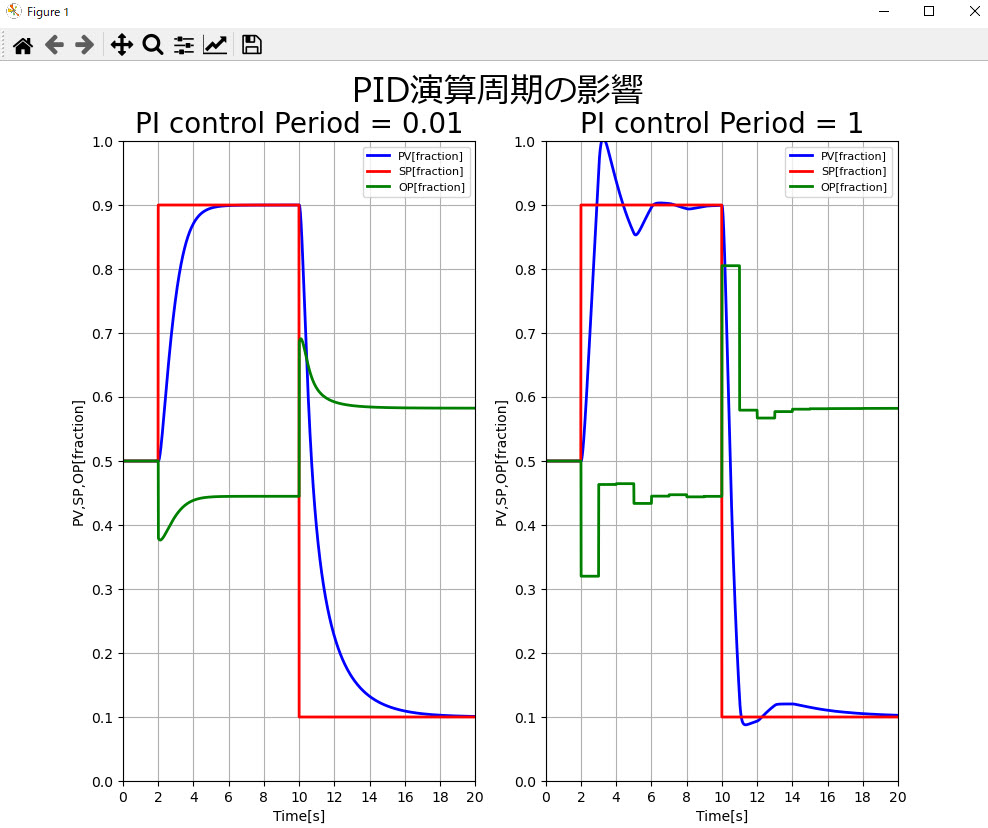
※計算条件:入口圧力120kPa、出口圧力100kPa、液密度一定とし1000kg/m3、入口流量1kmol/sで計算開始時は液面バランス状態。PIパラメーターはKp:0.3、Ti:2、バルブの時定数を2sec、計算時間刻みを0.01secとしています。
以前作成した簡単な制御の雰囲気を掴むためのモデルをご紹介します。
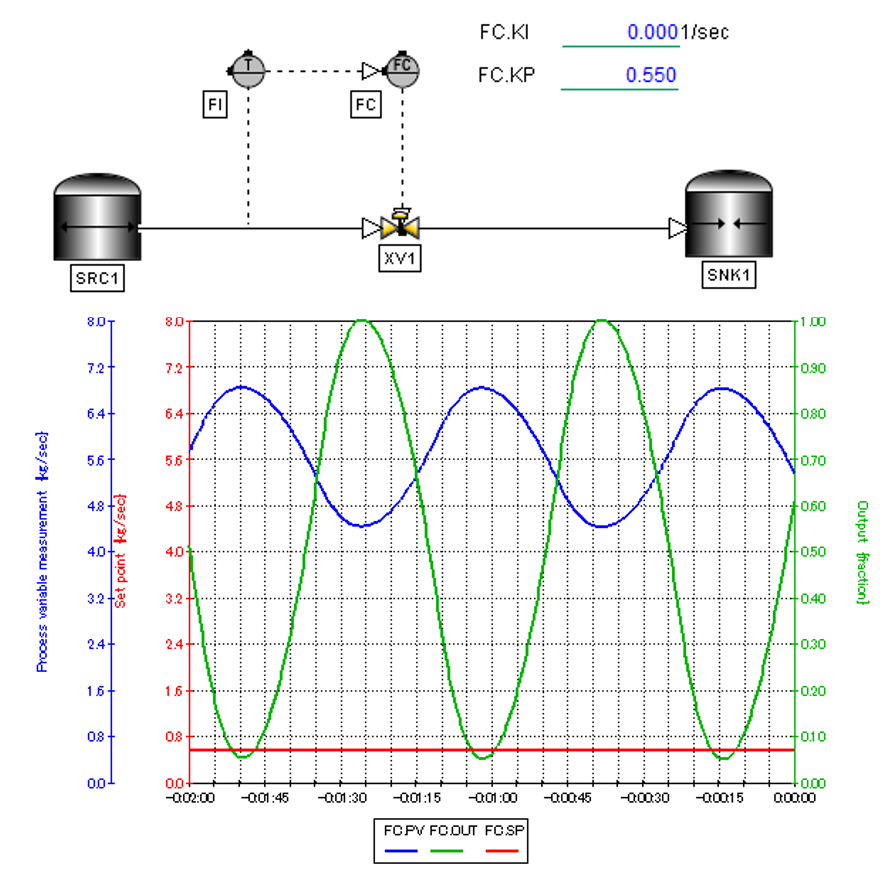
上図は、Transmitterに意図的に無駄時間と遅れ時間を設定し、Proportional項を調整して限界発振の状態を作り出しています。
通常のプラントでこのような状態を作り出すのは許されませんが、シミュレーション上であればこうした乱暴な操作も問題ありませんので、限界発振に必要なKp値を手探りで探すことができます。
限界発振の状態が分かればZiegler&Nicols限界感度法で適切なパラメーターを求めることができます。(限界感度法については制御のページをご参照ください)
以下は限界感度法でPIDパラメーターを決めた場合の制御過程を示しています。
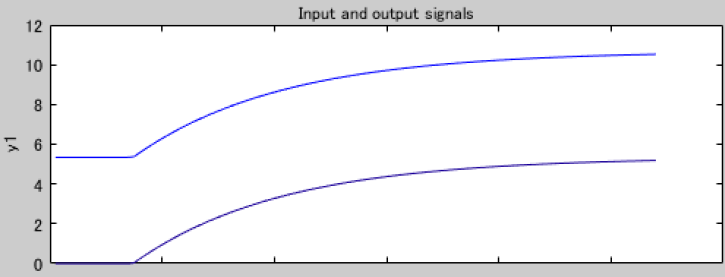
また、別のモデルですが、簡単なステップ応答テストをDYNSIM上で行い、Ziegler&Nicols過渡応答法を試してみたのが以下になります。
実機でステップ応答を見る場合には、大きな影響を与えない範囲を予め決めて、張り付きで状況を見ながら、なにかあればすぐにテストを中断しなければなりませんが、シミュレーターであれば、どんな外乱を与えても良いので、気楽に様々なテストを行うことができます。
DYNSIMで簡単なステップ応答テストを行い、結果をMatlabのSystem Identification Toolboxでシステム同定し、Control System toolboxで最適な制御パラメーターを決めた上で、DYNSIM上の挙動を見ていきます。
まず、DYNSIMの計算結果をデータヒストリアンからCSV形式で出力し、Matlabで読み込みます。
1点、注意点としてバイアスについてはシステム同定の前に除去しておく必要があります。
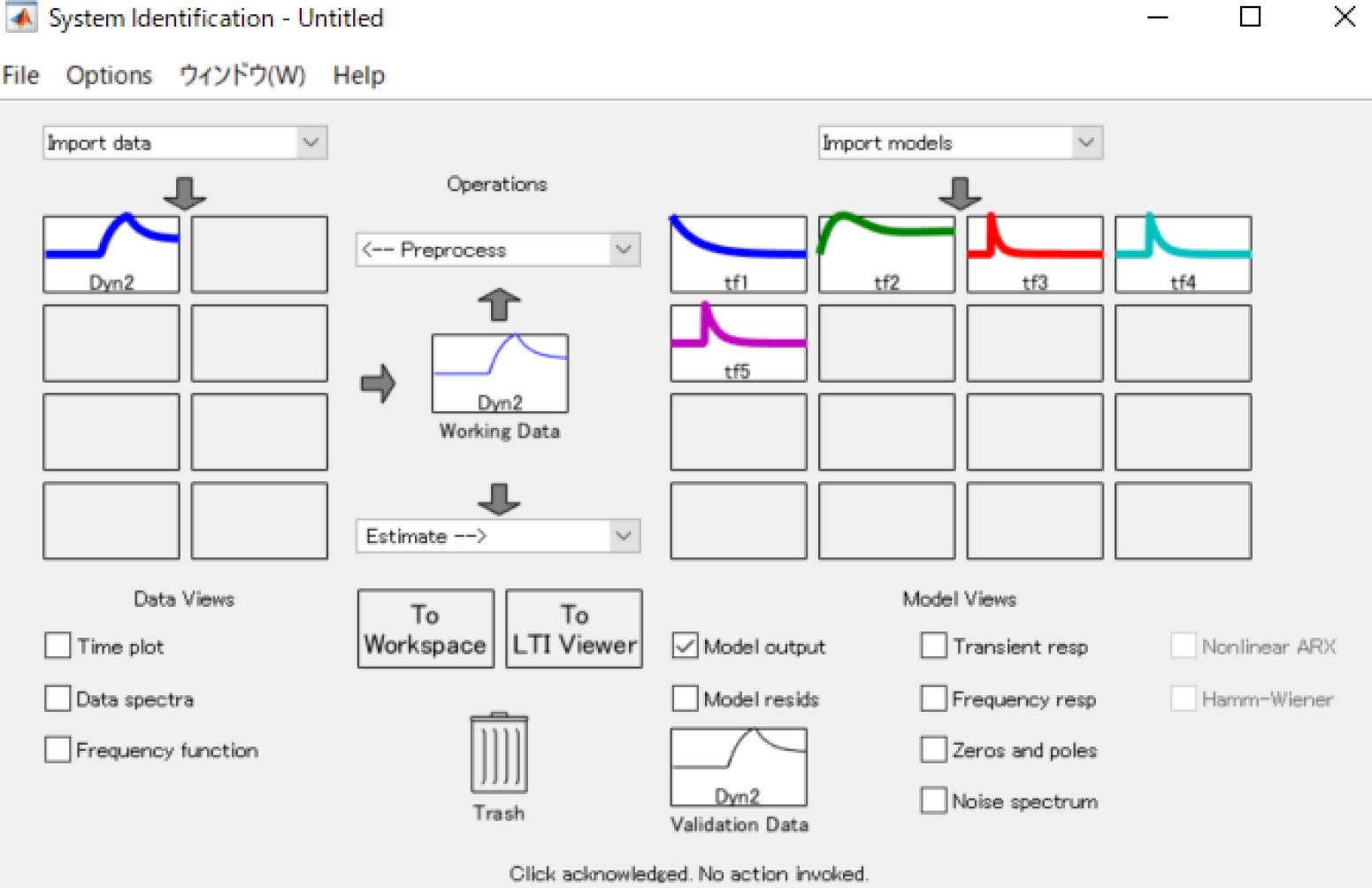
続いて、System Identification Toolboxを使ってシステム同定をします。
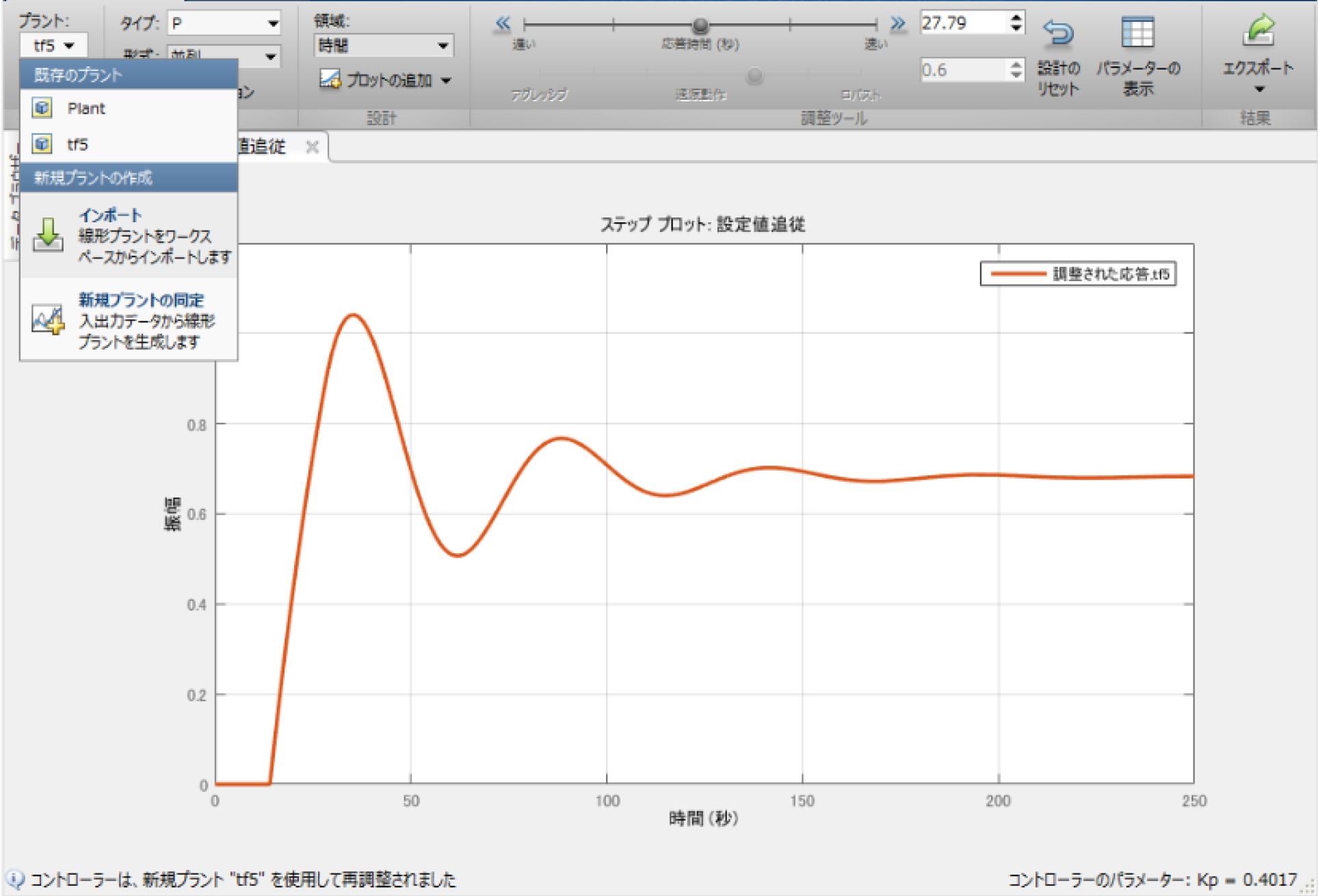
制御パラメーターをControl System Toolboxで決めていきます。
非定常シミュレーターで発散しやすい場面の一つに、ドラムやセパレーターユニットの液面が上昇していき、満液となるタイミングがあります。気相が無くなる瞬間、圧縮性流体から非圧縮性流体への取り扱いに切り変わり、フラッシュ計算のアルゴリズムが変わるため収束がし辛くなります。DYNSIMでは、この境界域を変更するパラメーターが用意されています。
DYNSIMでは、ホールドアップを有する殆どの機器(一部熱交換器等を除く)において、Holdupオプションとして、「No Holdup」、「Incompressible」、「Compressible」の選択が可能です。コンプレッサーのコーストダウン検討等、系内の圧縮性流体のホールドアップ量が重要なケースについて、IncompressibleやNoHoldupを選択してしまうと有意な検討結果が得られないので注意が必要です。
こちらでも記載しましたが、DYNSIMでは複数のPIDアルゴリズムを使うことができます。デフォルトではLegacyタイプというちょっと癖のあるアルゴリズムとなっているので、シミュレーションを開始する前に必ず見直すことをお勧めします。
こちらでも記載しましたが、DYNSIMでは計算の時間刻み幅と独立したPIDの演算周期を持たせることが可能です。上述のページに記載のように、PIDの演算周期が実機と異なっていると、計算結果が大幅に変わってしまうこともありますので、注意が必要です。
DYNSIMは、運転訓練シミュレーターのように、非常に大型のフローシート計算を高速で行うことができるよう、様々な工夫がなされています。その一つとしてフラッシュ計算の線形化オプションがあります。エンジン設定から線形化のON、OFFを切り替えることができるようになっています。スタートアップ検討等、非線形性の強いシミュレーションを行う必要がある場合は、線形化オプションをOFFにする必要があるケースもあります。また、計算時間刻みもこちらで記載したように安定性、計算速度に効いてくる部分になりますので、変更が必要となるケースがあります。
DYNSIMではユーザーがオリジナルのユニット(User Added Model)をC++で作ることができます。その際、次の環境変数が重要になります。DYNSIMのインストール時、システム環境変数のDSUAM_ROOTにインストールするDYNSIMのバージョンに応じたUAMフォルダの場所が書き込まれます。
異なるバージョンのUAMを作成する場合は、上記環境変数の書き換えが必要になるので、注意が必要です。
当サイトに不具合、ご意見等ございましたらCEsolutionにお知らせください。
