線形計画法は線形の制約条件下において、線形の目的関数を最小化あるいは最大化する条件を探索するために用いられます。

取り扱うことのできる問題設定としては、利益を最大化するための生産スケジューリングやタンク在庫調整、輸送問題等に用いられます。

例題として、Optimization for Chemical and Biochemical Engineeringで紹介されている4種の原油(1,2,3,4)から、３種の燃料（A,B,C）をブレンドする際の利益最適化問題を解いてみます。(ここでは問題設定の詳細は省略し、単に数式問題としてのみ解いておりますので、問題設定を確認されたい方は、上記の原著を当たられてください。)

原油、燃料の構成式 \begin{array} x_{A} = x_{1A} + x_{2A} + x_{3A} + x_{4A}\\ x_{B} = x_{1B} + x_{2B} + x_{3B} + x_{4B}\\ x_{C} = x_{1C} + x_{2C} + x_{3C} + x_{4C}\\ x_{1} = x_{1A} + x_{1B} + x_{1C}\\ x_{2} = x_{2A} + x_{2B} + x_{2C}\\ x_{3} = x_{3A} + x_{3B} + x_{3C}\\ x_{4} = x_{4A} + x_{4B} + x_{4C}\\ \end{array} 各原油、燃料ブレンドレシピの制約式 \begin{array} x_{1} \leq 1000\\ x_{2} \leq 3000\\ x_{3} \leq 2000\\ x_{4} \leq 1500\\ x_{1A} \leq 0.25x_{A}\\ x_{2A} \leq 0.35x_{A}\\ x_{3A} \leq 0.55x_{A}\\ x_{1B} \leq 0.45x_{B}\\ x_{2B} \leq 0.2x_{B}\\ x_{1C} \leq 0.6x_{C}\\ \end{array}

また、各xij、xi、xjは非負数

目的関数 6.0x_{A} + 4.0x_{B} + 3.0x_{C} - 2.0x_{1} - 5.0x_{2} - 6.0x_{3} - 3.0x_{4}

LP問題はPythonでいくつか便利なモジュールがあり、正規形に変換しなくても、そのまま簡単に解くことができます。試しにcvxpyで求めてみると、解は10923と求まりますが、上記の著書にも解が載っていないため、以下モジュールを使わずにSimplex法で検算してみます。

Levenberg-Marquardt法は非線形最小二乗問題の解法としてよく用いられます。

実験データとのフィッティングや非線形方程式の解法として非常に優れた方法です。Pythonを使う場合はleastsq関数で呼び出すことが可能です。以下シンプルな問題設定について、まずleastsq関数で解を求め、その後ベタ打ちのコードで検算をしていきます。

シンプルな例題

例として、仮に以下のような反応データが得られたと仮定して、power law型のn次反応にフィッティングしてみます。

シンプルな例題

例として、以下の等式制約付きの最適化問題を解いてきます。（等式制約１つの例）

$$ P:min f(x,y) = -x^3 - 3xy^2 + y^3 + 3x $$ $$ s.t. g(x,y) = x^2 + y^2 -1^2 = 0 $$

まず、ラグランジュ乗数λを用いた以下のラグランジュ関数Lを用意します。

$$ L(x,y,\lambda) = f(x,y) + \lambda g(x,y)$$

ラグランジュ乗数法: \( \nabla L(x,y,\lambda) = 0\)より制約付き停留点の式は以下となります。

$$ \frac{\partial L}{\partial x} = -3x^2 -3y^2 +3 -2\lambda x = 0 $$ $$ \frac{\partial L}{\partial y} = -3y^2 -6y -2\lambda y = 0 $$ $$ \frac{\partial L}{\partial \lambda} = x^2 + y^2 - 1 = 0 $$

以下は、初期値[] = (0, -0.1, -2.0)からNewton法で計算した場合の計算の軌跡になります。

実用的な例題

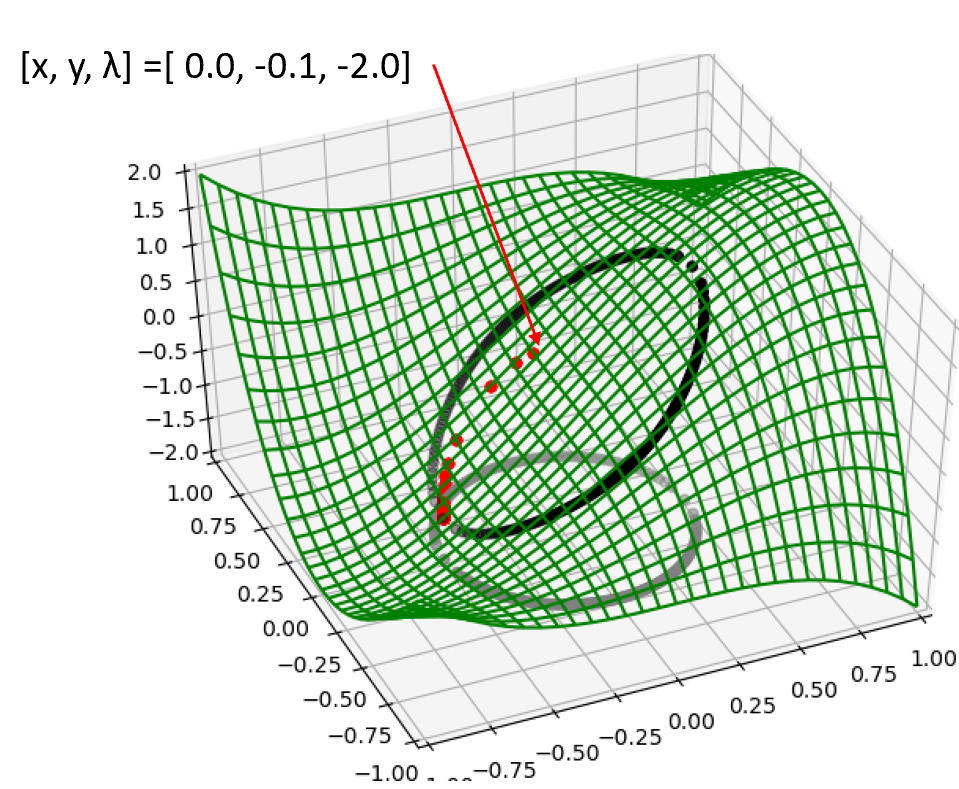
Lagrange未定乗数法は、化学工学問題の色々な場面で役立ちます。反応のページでご紹介しているGibbs反応器やデータリコン等で活用できます。

逐次２次計画法（SQP: Sequential quadratic programming）は等式、不等式制約付きの最適化問題幅広く使われている手法です。非線形の関数に対しても適用可能です。

シンプルな例題

以下Rosenbroch関数の最小値の探索を、まずはScipyのminimize関数、method =SLSQPを使って求めます。

$$ P: a(x_2 - x_1^2)^2 + (b - x_1)^2$$ $$ s.t. x_1 \leq 0.9, x_2 \leq 1.5 $$

ただし、a = 10, b = 1とし、初期値[-1.0, 1.2]からスタートします。

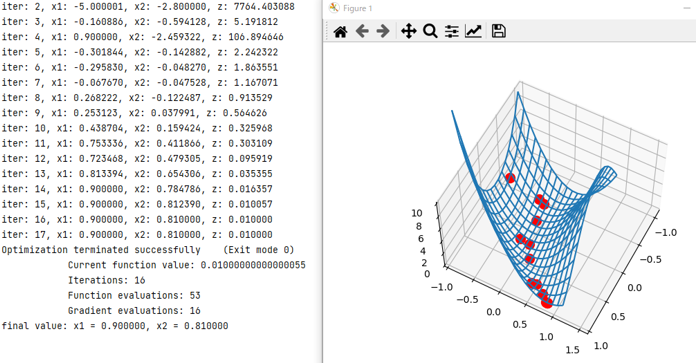
まず結果を示しますが、SLSQPを用いて求めると、14回目以降、x1の不等式制約に先にぶつかり、そこからx2を変えつつ、最小値に到達している状況が確認できます。

実用的な例題

準備中。

化学工学の問題を取り扱う上で、製品品質vs製造コストや環境負荷vs製造コストのように互いにトレードオフの関係にある目的変数を最適化する必要のあるケースがあります。ESTECO社のmodeFRONTIER以外にも多目的最適化のソフトはありますが、個人的に優れていると思うmodeFRNTIERについて以下にまとめていきます。

ただし、ソフトの使い方については、ソフトウェアベンダーが提供している有料のトレーニング等がございますので、そちらをご活用ください。（HP上でソフト内のパラメーターや内部式の細かいところを載せるわけにはいきませんので、ご了承のほど宜しくお願いします。）また購入方法等についても、当HPで取り扱っているわけではありませんので、ソフトウェアベンダー（日本国内ではIDAJ社）に直接お問い合わせください。

modeFRONTIERの例題として取り上げられている梁断面の構造最適化の例で見ていきます。

問題設定、設定方法については、modeFRONTIERのTutorialのGetting Startedをご参照ください。

Tutorial1の設定完了段階の図が以下になりますが、以下のようにGUIからフロー図を作り、視覚的に問題構成が分かるようになっています。csvやExcelからの入力、バッチコマンドの挿入等もブロックで行うことがあり、こちらも視覚的に操作ができるように工夫がなされています。

設定の容易さもさることながら、出力が非常に素晴らしいです。多目的最適化の場合、最終的にどのパラメーターを採用するべきかを判断する必要がありますが、多様なグラフ出力がデフォルトで用意されており、こちらも視覚的に判断ができるように工夫されています。

以下modeFRONTIERで使用できるグラフをいくつかご紹介します。