Scilabの初期画面

Scilabからアプリケーション→SciNotesでPythonのようなスクリプト形式のファイル画面が表示されます。VBEditorのように、変数ブラウザで、常に途中の数値が確認できるのが有難いです。

再生ボタンを押すと、記載したスクリプトを実行することができます。

ATOMS

また、以下ATOMSから、様々なモジュールをダウンロードすることが可能です。

基本コマンド

・コンソール画面への出力

disp()コマンドを使用

disp("Hello")

出力 ： Hello

・コメントアウト

入力 ： //

・変数の代入

　例えば、a、bという２変数にそれぞれ1、3を代入する場合、

・論理演算子

andやorはそのまま使用することが可能です。

・行列計算の演算子

ベクトル・行列

転置

・複素数の表現 　

複素数、共役複素数、複素数の絶対値の入力例（上記のa,bの入力に続けて以下入力下さい）

　

↓虚数部の表現　：　%i、　共役複素数　：　conj()、 絶対値 ： abs()

　

↓絶対値の計算確認ついでに平方根の入力確認 ： sqrt()

　

↓指数計算もできます。 ： exp()

　

ここまで分かれば周波数特性G(jω)の計算も楽々です。例えば、1次遅れ+無駄時間を確認してみます。

　

1次遅れ時間τ=10sec、無駄時間：DT=5secとして確認してみます。1次遅れ+無駄時間の伝達関数は、

$$G(s)=\frac{K \cdot exp\left(-DT \cdot s\right)}{\tau \cdot s +1}$$ $$G(s)=\frac{exp\left(-5 \cdot s\right)}{10 \cdot s +1}$$

sにjwを入れると、

$$G(jw)=\frac{exp\left(-5 \cdot j \omega \right)}{10 \cdot j \omega +1}$$

ω=0.1, 1, 10, 100の時のG(jw)を見てみます。

ω=0.1, 1, 10, 100を行列に格納します。配列は以下のように簡単に宣言できます。

各ωに対するG(jω)は、for文で求めます。for文は、for a:b ～ endとします。

　

・sceファイルをサブルーチンとして呼び出す方法

excec('ファイルパス')の形で呼び出しが可能です。

例)excec('vpcalc.sce')

例えば、蒸気圧推算は、成分によって式形が異なるので、メインプログラム側では記載せず、サブルーチン側で処理した方がコードが長くならずスッキリします。

　

　

例として、以下の伝達関数について、①根軌跡、②Bode線図、③Nyquist線図、④Nichols線図をプロットする方法を示します。

$$f(s)=\frac{3\left(s-1\right)}{s(s+2)(s+5)}$$ 　

まず上記の伝達関数を定義しおきます。

s=poly(0,'s');
P = syslin('c',3*(s-1)/(s*(s+2)*(s+5)));

　

①根軌跡

evans(P);

　

②Bode線図

bode(P);

　

③Nyquist線図

nyquist(P);

　

④Nichols線図

black(P);

ScilabでのBode線図、Nyquist線図の作成方法についてはこちらもご参照ください

　

例えばcsvファイルに基本物性データを入力しておき、read関数で読みこむ場合、以下のように設定します。（パスは絶対パスでもＯＫです）

　

以下のようにcsvファイルが読み込まれます。

　

例えばωのデータをOMEGAに代入したい場合、OMEGA=[Sheets(1,1) Sheets(1,2) Sheets(1,3)]のように、該当する行列番号を指定してやります。

　

2d plotの作成

グラフの作成例として、お決まりの３次方程式を題材とします。

状態方程式法の解法の詳細についてはこちらをご参照ください。

ここでは既に状態方程式法を３次方程式形まで持っていけることを前提に話を進めます。

Scilabでは３次方程式の解はroots()関数を使うことで簡単に求められます。

以下はSRKのzを求める場合の例になります。

y1=x.^3-x.^2+(Aa(1)-Bb(1)-Bb(1).^2)*x-Aa(1)*Bb(1)
roots(y1)

以下のように複素数解も求まります。

グラフ表示させたい場合は、以下のようにplot2d()で表示できます。

以下の例では、３通りの圧力、温度でz-f(z)のプロットを重ねて表示しています。

plot2d(x,[y1' y2' y3'],[1 2 3]);
xgrid()
xtitle('z diagram','z','f(z)')
hl=legend(['case1';'case2';'case3'],,3)

3d plotの作成

基本的な3d plotはplot3d()で表示できます。

※参照：Introduction to Scilab

x = linspace(1,%pi,30)
y = linspace(1,%pi,30)
z = sin(x)'*cos(y)
plot3d(x,y,z)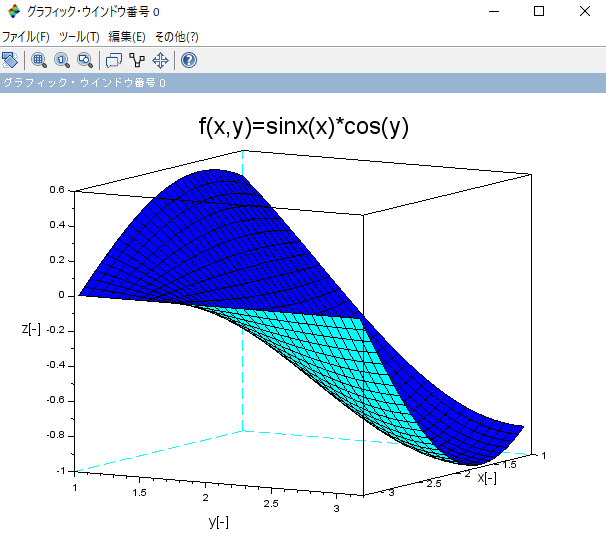

なお、グラフは右クリックしながら回転させることも可能です。

位相進み補償の表現 微分方程式の解法 ・ode関数

ode関数のタイプとして選択できるのは、以下の通り。

"adams" "stiff" "rk" "rkf" "fix" "discrete" "roots"

例題として、Pythonでも確認した硬い問題を試してみます。（Van Der Pol方程式）

比較前提

Time step:0.1[sec]、積分時間：2000[sec]、μ:1000

van der pol方程式は以下の通り。

$$\frac{d^2x}{dt^2}-\mu \left(1-x^2\right)\frac{dx}{dt}+x=0$$

初期値定義

X0 = [2.0; 1.0];

ode関数定義.以下のvanderpolが関数定義部になります。

[X] = ode("stiff",X0,0,T,vanderpol);

1次遅れのステップ応答

まずは最小構成の１次遅れプロセスへのステップ応答です。

メニューバーのアプリケーション→XCOSを起動します。

パレットブラウザから以下のユニットを配置し、フローシートを作成してきいます。

なお、以下の構成は10秒間の応答を見るだけの構成になっておりますので、必要に応じてCSCOPEのRefresh periodや積分時間は見直してください。

グループ	ユニット名	設定１	設定２
信号源	Step_FunctionL	ステップ時間：0	初期値：0、最終値：1
連続時間システム	CLR	Numerator：1	Denominator：1+T*s
出力/表示	CSCOPE	Refresh period：10	-
信号源	CLOCK_c	間隔：0.1	初期化時間：0.1

シミュレーション→設定→積分終了時間を1.0E01に変更します。

※Defaultでは1.0E5となっているので、このままでは単位ステップの応答は確認できません

例えば遅れ時間10secの場合、Scilabのコンソール画面でT=10とし、開始ボタン（再生マークです）を押して計算を開始します。

遅れ時間として設定した10secで、出力が1-1/eとなっていることが確認できます。

2次遅れのステップ応答

続いて２次遅れプロセスへのステップ応答です。

折角なので、１次遅れとの違いが見やすいように、入力信号と、１次遅れ、２次遅れの出力をまとめて一つのプロットで出してみます。（失敗過程も含めて以下記載します）

・１回目のトライアル(CMSCOPEを使ってみる)

・２回目のトライアル、、、(CSCOPEの出力ウィンドウを揃えてみる)

・３度目の正直！(MUXを使う)

XcosのマニュアルにXcosのバッチランについてのコマンドがありましたのでご紹介します。

XcosをScilabからバッチ実行することで、Bode線図をXcosファイルから作成することができるようです。

詳細は、ブログにまとめたのでこちらをご参照ください。

以下のように、XcosからBode線図を作成することができます。