反応の基本

液相反応の場合、頻度因子A[1/sec]、活性化エネルギーE[kJ/kg-mol]、反応温度T[K]、成分Aに対してn次、成分Bに対してm次反応で、成分A、Bの液相濃度をそれぞれ$C_A$[kg-mol/m3]、$C_B$[kg-mol/m3]とすると、成分Aの反応速度$r_A$[kg-mol/sec-m3]は以下の式で表されます。

$$-\frac{r_A}{a}=A \cdot exp\left(-\frac{E_f}{RT}\right) \cdot C_A^n \cdot C_B^m \tag{1.3}$$

成分B、C、Dの反応速度については式(1.2)の関係から求めることができます。

また、気相反応の場合は成分A、Bの分圧がそれぞれ$p_A$、$p_B$であったとすると、反応次数、反応条件、反応定数が同じであれば（頻度因子の単位は異なります）、以下の形で表されます。

$$-\frac{r_A}{a}=A \cdot exp\left(-\frac{E_f}{RT}\right) \cdot p_A^n \cdot p_B^m \tag{1.4}$$

べき乗則に基づく反応速度は正反応を添え字f、逆反応を添え字rで表すと、0次反応の場合は、以下の式形で表されます。

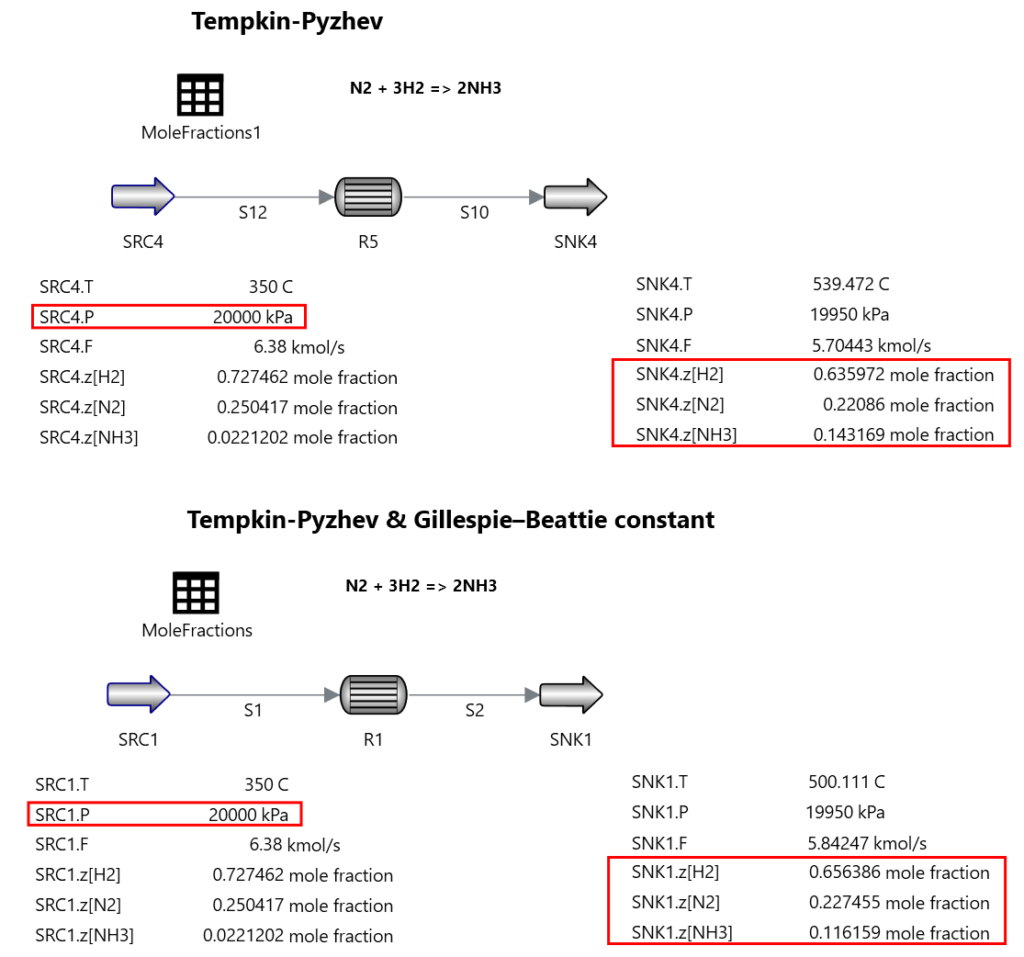
$$r=A_f \cdot exp\left(-\frac{E_f}{RT}\right)-A_r \cdot exp\left(-\frac{E_r}{RT}\right) \tag{1.5}$$

具体的な反応例として、以下アンモニア生成反応の例を紹介します。

Temkin and Pyszhevの反応モデル(1940)を使用します。N2基準の反応で、

$$ r[N_2] = k_1 \left( \frac{p_{N_2}p^3_{H_2}}{p^2_{NH_3}} \right)^{\alpha} - k_2 \cdot \left( \frac{p^2_{NH_3}}{p^3_{H_2}} \right)^{\alpha}$$

ここで、鉄系触媒の場合は、α=0.5

以下Annable (1952)のパラメーターを使います。

$$ k_1 = k_{1o} exp(-20800 / RT)$$ $$ k_2 = k_{2o} exp(-47400 / RT)$$ $$ k_{1o} = 1.78954 \cdot 10^4 [kmol / m^3 catalyst bed - hr]$$ $$ k_{2o} = 7.143 \cdot 10^{16} [kmol / m^3 catalyst bed - hr]$$

void率をε[-]、反応器容積をV[m3]とすると、N2の反応速度[kg-mol/sec]は、

$$ rate[N_2] = \epsilon V \left[ k_1 \cdot \left( \frac{p_{N_2} p^{1.5}_{H_2}}{p^2_{NH_3}} \right) - k_2 \cdot \left( \frac{p_{NH_3}}{p^{1.5}_{H_2}} \right) \right]$$

出典

S. S. E. H. Elnashaie & S.S.Elshishini “Modelling, Simulation and Optimization of Industrial Fixed Bed Catalytic Reactors”, Page. 98, equation 3.163

もう少し詳細な反応モデルとして、こちらのBernieさんの論文で紹介されているGillespie–Beattie correlationを使った反応モデルもあります。

こちらのページでAVEVA Process Simulationを使った場合のモデリング例を紹介しています。

LHHW（Langmuir-Hinshelwood-Hougen-Watson)

不均一触媒の表現としてLHHW式があります。LHHW式は、原料物質の吸着、触媒表面での反応、反応物質の脱離を考慮したモデルとなっており、反応速度の寄与項、平衡からのズレを考慮したdriving-force項、触媒表面の被覆を考慮した吸着を表現する項からなっています。

反応を考慮した物質収支、熱収支

以下条件の反応器における熱収支、物質収支を考えます。

一般的な物質収支式

$$F_{in}\cdot z_{in} - F_{out}\cdot z_{out} + Rate = \frac{d z_{out}}{dt} \tag{1.6} $$ 一般的な熱収支式

$$F_{in}\cdot H_{in} - F_{out}\cdot H_{out} + Rate = \frac{d H_{out}}{dt} \tag{1.7} $$

ここで、F：モル流量[kmol/sec]、z：モル組成[fraction]、Rate：反応量[kmol/sec]、H[kJ/sec]：エンタルピー、Duty：外部からの入熱[kJ/sec]、Hr[kJ/sec]：反応熱、添え字のin、outはそれぞれフィード、プロダクトを表しています。

定常状態における物質収支

定常状態においては、濃度変化が0となるため、

$$F_{in}\cdot z_{in} - F_{out}\cdot z_{out} + Rate = 0 \tag{1.8} $$

定常状態における熱収支

定常状態においては、エンタルピー変化が0となるため、

$$F_{in}\cdot H_{in} - F_{out}\cdot H_{out} + Duty + Hr = 0 \tag{1.9} $$

完全混合反応器

完全混合反応器:Continuout Stirred Tank Reactor(CSTR)は反応器内が瞬間的に十分に混合され、反応器内で組成分布を持たないと考えられることが前提となっています。

CSTR内は定常状態と考えられますので、(1.8)の式において、単位容積当たりの反応速度をr[kmol/sec-m3]、反応器容積を[m3]とすると、物質収支式は下式で表されます。

$$F_{in}\cdot z_{in} - F_{out}\cdot z_{out} + r \cdot V = 0 \tag{1.10} $$

(1.9)式より、CSTRの設計式は下式で表されます。

$$V = -\frac{F_{in}\cdot z_{in} - F_{out} \cdot z_{out} } {r} \tag{1.11} $$

押し出し流れ反応器

押し出し流れ反応器:Plug Flow Reactor(PFR)は長手方向に向かって組成が変化していきます。反応器内を複数セグメントに分割し、各セグメント内は完全混合であると考えます。

今、管型反応器の断面積をA[m2]（長手方向に管径は一定、鏡部はフラットとする）、長さをL[m]とし、反応器を長手方向にN分割します。今、i番目のセグメントにおける単位容積当たりの反応速度をr_i[kmol/sec-m3]とするとセグメントiにおける物質収支は下式で表されます。

$$F_{in, i} \cdot z_{in, i} - F_{out, i} \cdot z_{out, i} + r_i \cdot A \cdot L / N= 0 \tag{1.12} $$

上式をi=1～Nまで

回分反応器

回分反応器は

準備中

触媒反応器の圧力損失計算

Ergun式

乱流域で使用できる一般的な圧力損失計算式としてErgun式があります。

Ergunタイプの圧力損失計算式はいくつかあり、以下に記載されているfの係数が異なっていますが、特にErgun(1952)式は以下の領域で使える式となっています。

$$ \Delta P = \frac{fZ \rho V_s^2 ( 1 - \epsilon )}{D_p \epsilon^3} $$ $$ f = \frac{150}{Re} + 1.75 $$ $$ Re = \frac{D_p V_s \rho}{(1 - \epsilon) \mu} $$ $$ 球形粒子ではない場合 : D_p = \frac{6V_{particle}}{As_{particle}}$$ $$ 適用範囲　: \frac{Re}{1 - \epsilon} \lt 5000 $$

ここで、

Z ；Length of the bed

DP ；Equivalent spherical diameter

μ ；Fluid viscosity

ρ ；Density of Fluid

VS ；Superficial velocity

ε　；Void fraction of the bed

なお、上式では代表粒径を粒子の体積、表面積から求めていますが、円柱形粒子に対しては異なる式も提案されています。

参考 : Sabri, Ergun, “Fluid Flow Through Packed Columns,” Chemical Engineering Progress, Vol. 48, No.2, 1952, pp. 89-94

また、圧力損失計算に関してはこちらの本が参考になります。

反応器の温度コントロール

冷却速度と反応熱

温度コントロール

触媒の劣化速度

化学工学便覧記載の劣化速度推算式についてまとめていきます。

準備中

Gibbs Minimization反応器

Gibbs Minimization反応器は、ある温度、圧力においてGibbs自由エネルギーが最小となる平衡組成を求めます。

反応定数を求められない場合や燃焼反応等で簡易的に用いられます。

問題設定としては、以下の等式制約付き最適化問題を解く形となります。

等式制約付き最適化問題の解法としては、最適化のページで紹介しているLagrange未定乗数法が挙げられます。

$$ P\ : min G(n_i, T, P) $$ $$ s.t. \ : nin_j - nout_j = 0$$

ただしここで、iは成分数、jは元素数

Lagrange Multiplierで上式を解く場合、等式条件を組み込んだ以下L(λ,n)を最小化する問題と置き換えることができます。

$$ min \ L(\lambda, n) \equiv G(n) - \lambda^T (nin - nout)$$

上記のL(λ,n)をそれぞれλ,nで偏微分した以下の連立方程式を解くことで、平衡組成を求めることができます。

$$ \frac{\partial L}{\partial n} = 0$$ $$ \frac{\partial L}{\partial \lambda} = 0$$

上式まで落とし込めれば、scipy.optimizeのfsolveである程度解けます。（収束しづらい場合、初期値の見直しが必要な場合もあります）

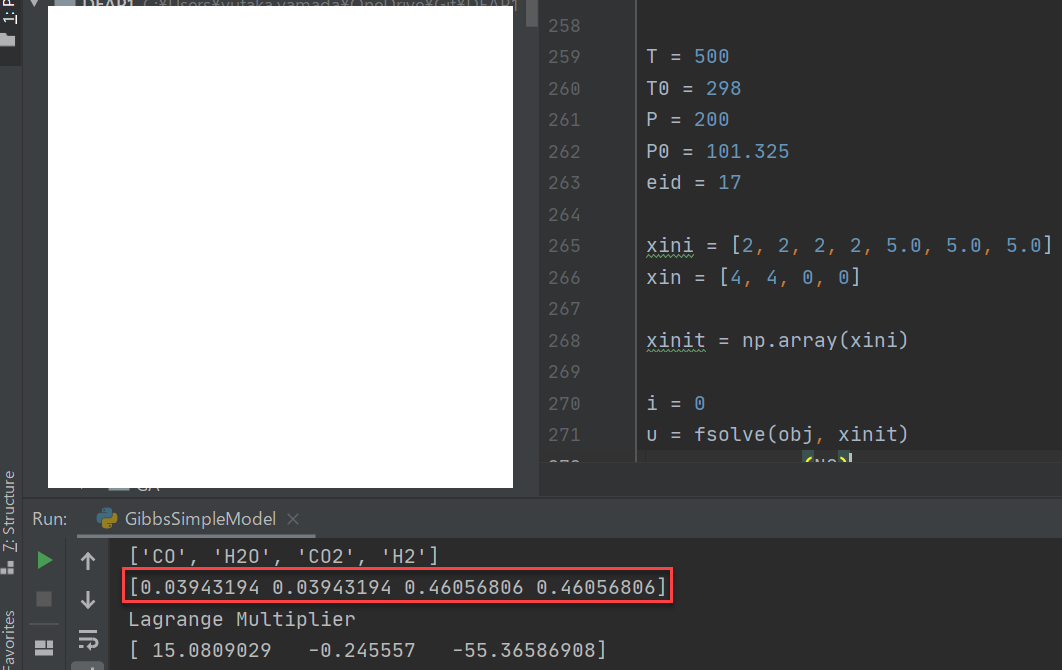
上図は以下のFeed温度、圧力、組成で計算させたシフト反応（等温反応）の例になります。

温度：500[K]、圧力：200[kPa]、z[CO]：0.5, z[H2O]：0.5, z[CO2]：0.0, z[H2]：0.0

シミュレーターでは反応定数、量論数もなにも入力しなくて良いので、非常に簡単な設定で計算を開始することができます。

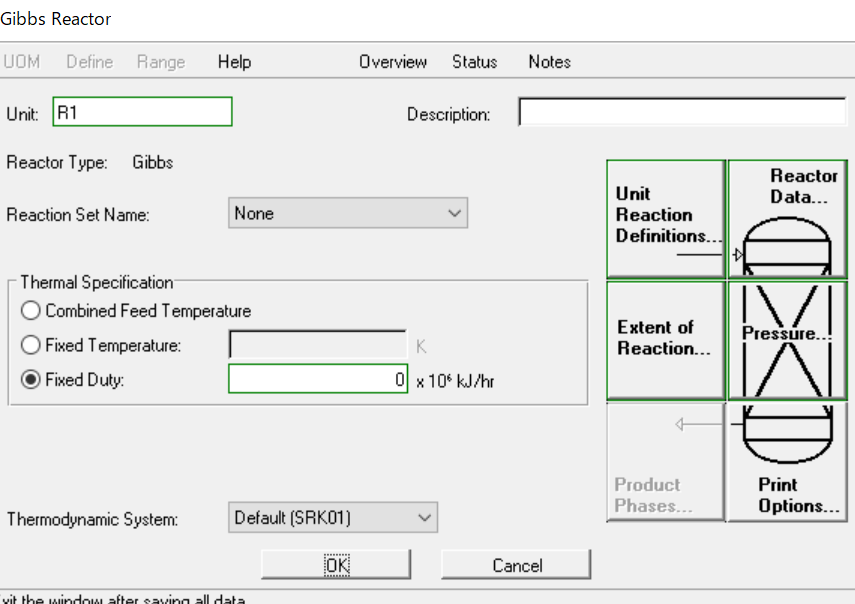
以下はAVEVA社のPRO/IIのGibbs反応器の入力画面ですが、ほぼデフォルト設定のままランさせるだけで計算できます。（断熱反応器とするために、Dutyにスペックを付け替えています）

以下参考としてCOFEのExampleにあるCumene反応を、Gibbs反応器に置き換えて、PRO/IIのGibbs反応器の計算結果と比較した際の計算例です。（断熱反応です）

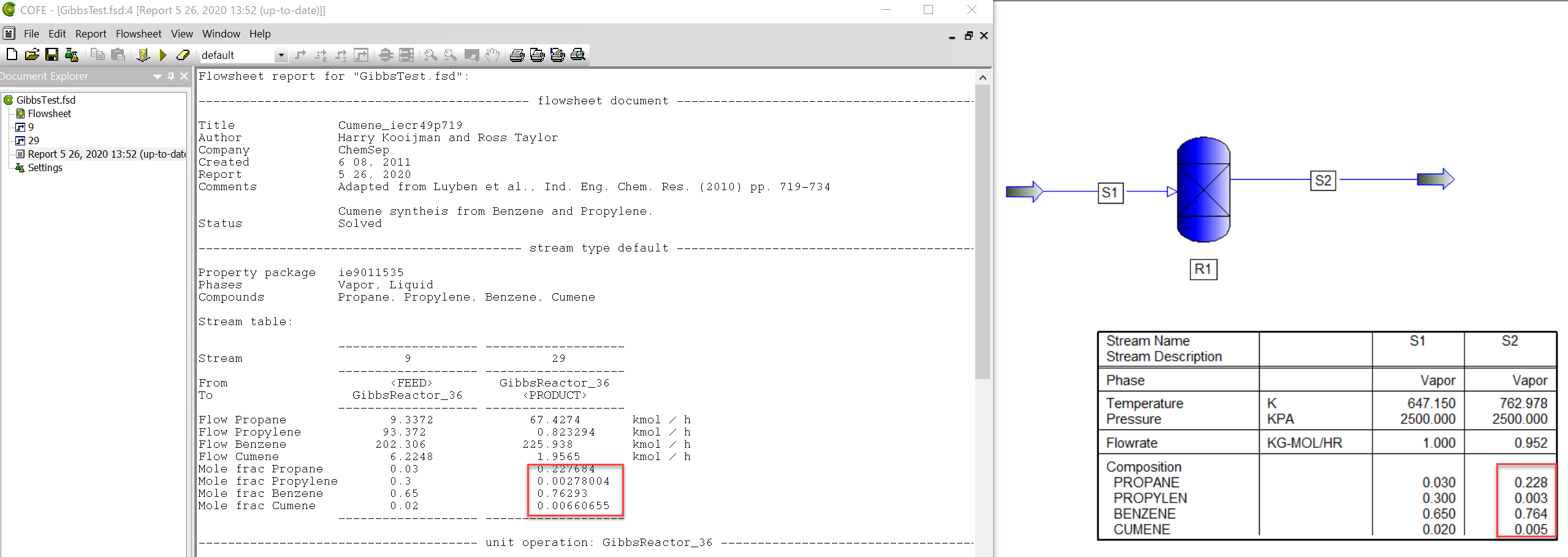
Feedの温度、圧力、組成は以下になります。（流量は合わせていません）

温度：374[K]、圧力：2500[kPa]、z[PROPANE]：0.03, z[PROPYLEN]：0.3, z[BENZENE]：0.65, z[CUMENE]：0.02

ほぼ同様の結果が得られています。

当サイトに不具合、ご意見等ございましたらCEsolutionにお知らせください。