CV値の定義

Cv値はバルブ容量を表す係数で、60°Fの水をCv[gal/min]流した時の圧損が1[lbg/in2]となります。

Cv値は、K値と以下の関係があります。（K値については、配管の圧損計算->代表的なFitting類のK値をご参照ください）

$$C_v=\frac{29.9 \cdot d^2}{\sqrt K}$$

なお、dはバルブポート径[inch]になります。

非圧縮性流体のCVサイジング(乱流域)

・亜音速域のサイジング : \(\Delta P \geq F_L^2(P_1-F_FP_V)\) $$C=\frac{Q}{N_1} \cdot \sqrt{\frac{\rho_{in} / \rho_0}{\Delta P}}$$ ・超音速域のサイジング $$C=\frac{Q}{N_1 F_L} \cdot \sqrt{\frac{\rho_{in} / \rho_0}{P_{in} - F_F P_v}}$$

※\(N_1 : 8.65E^{-2}[-] , Q[m^3/hr], P[kPa]\)

※\(\rho_0 \): 15C, 1atmにおける水の密度

※\(F_L \): Liquid Pressure Recovery Factor (グローブ弁で0.8～0.9程度。各種バルブタイプに対する値はISAのテーブル確認)

※\(F_F \): Liquid Critical Pressure ratio factor (\(0.96-0.28 \sqrt {\frac{P_v}{P_c}}\)で近似可能)

圧縮性流体のCVサイジング(乱流域)

・亜音速域のサイジング : \(x \lt F_r x_T\) $$ C = \frac{W}{N_6 Y \sqrt{x P_1 \rho_1}} $$

※\(N_6 : 2.73[-] , W[kg/hr], P[kPa]\)

※\(x_T\): pressure differential ratio factor (グローブ弁で0.7程度、各種バルブタイプに対する値はISAのテーブル確認)

※Y: Expansion factor

$$ Y = 1 - \frac{x}{3F_{\gamma}x_T}$$

ただし、\(x \geq F_r x_T\)の時、つまり超音速域においてはYは0.667

・超音速域のサイジング : \(x \geq F_r x_T\) $$ C = \frac{W}{0.667N_6 Y \sqrt{F_r x_T P_1 \rho_1}} $$

参照：IEC(International Electrotechnical Commission) 60534-2-1

バルブ特性

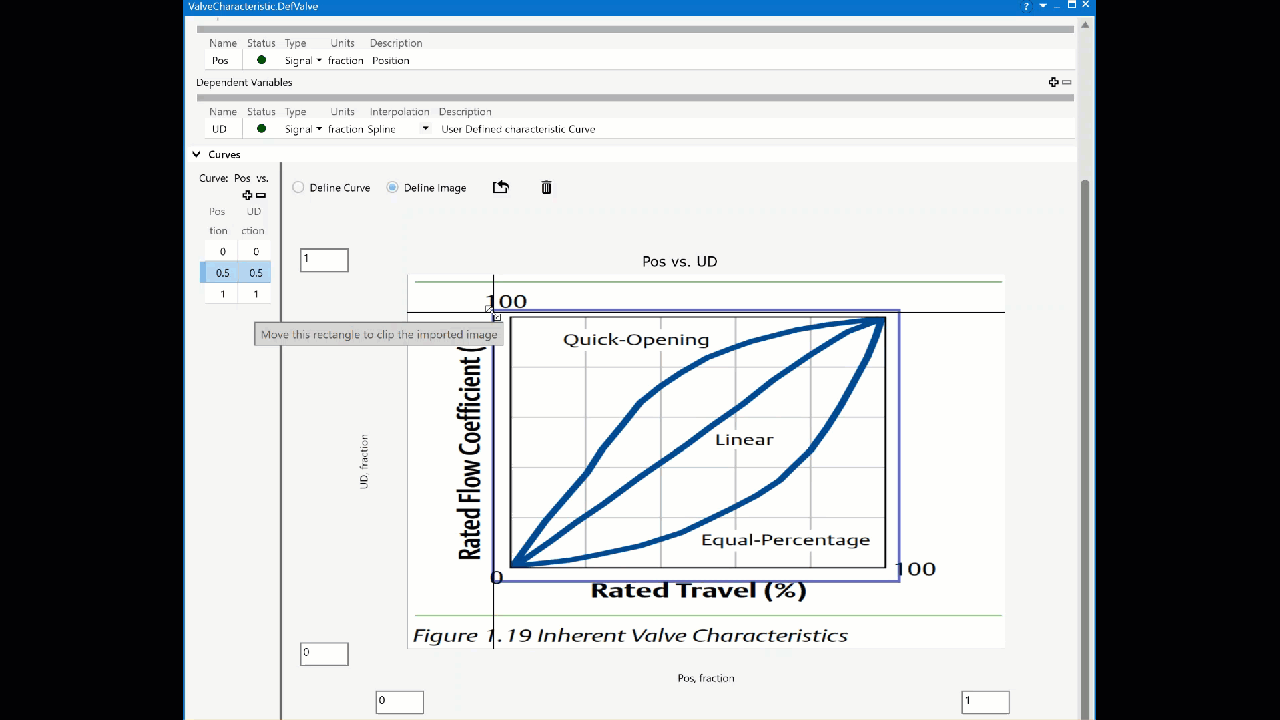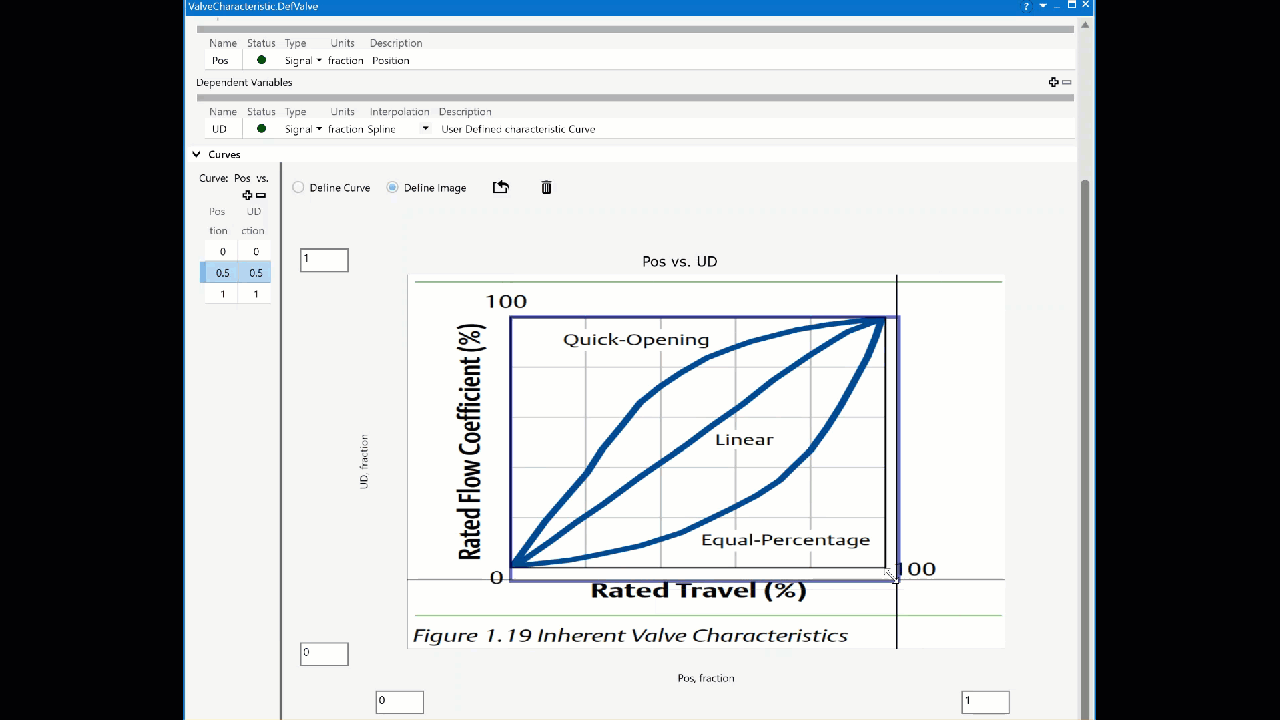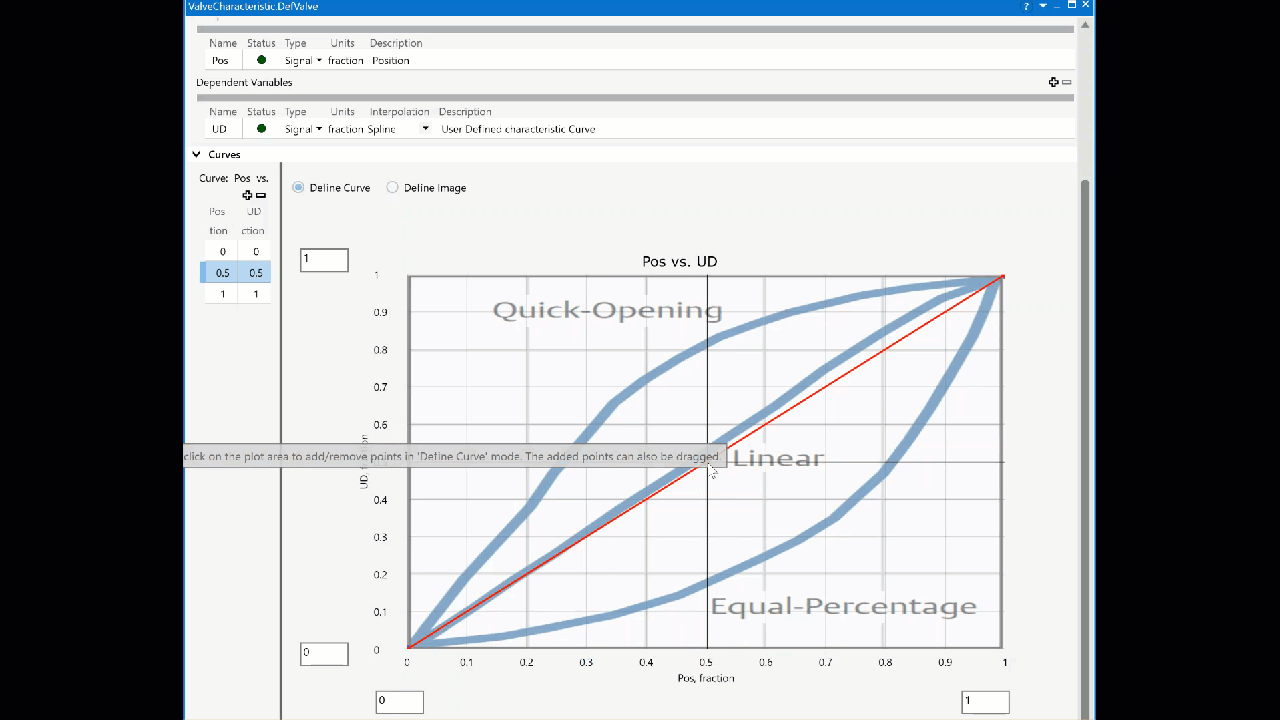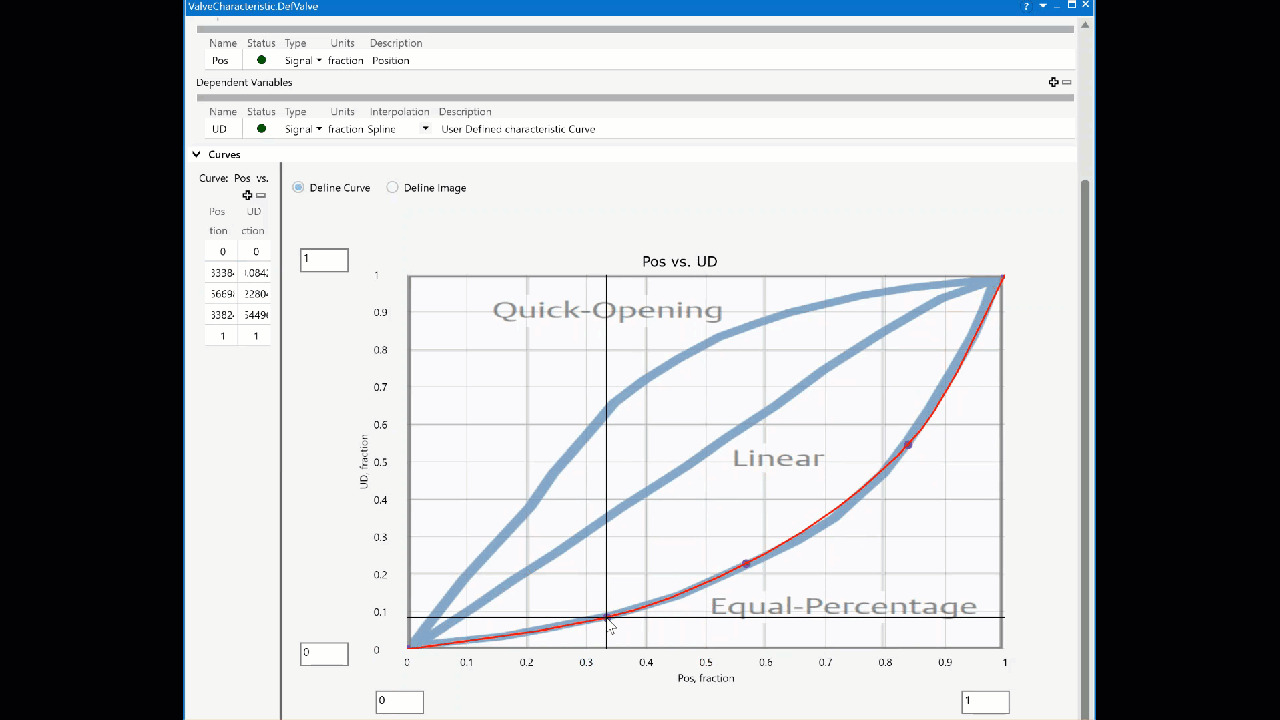
EmersonのHPに、代表的なバルブタイプに応じた特性線図が記載されています。

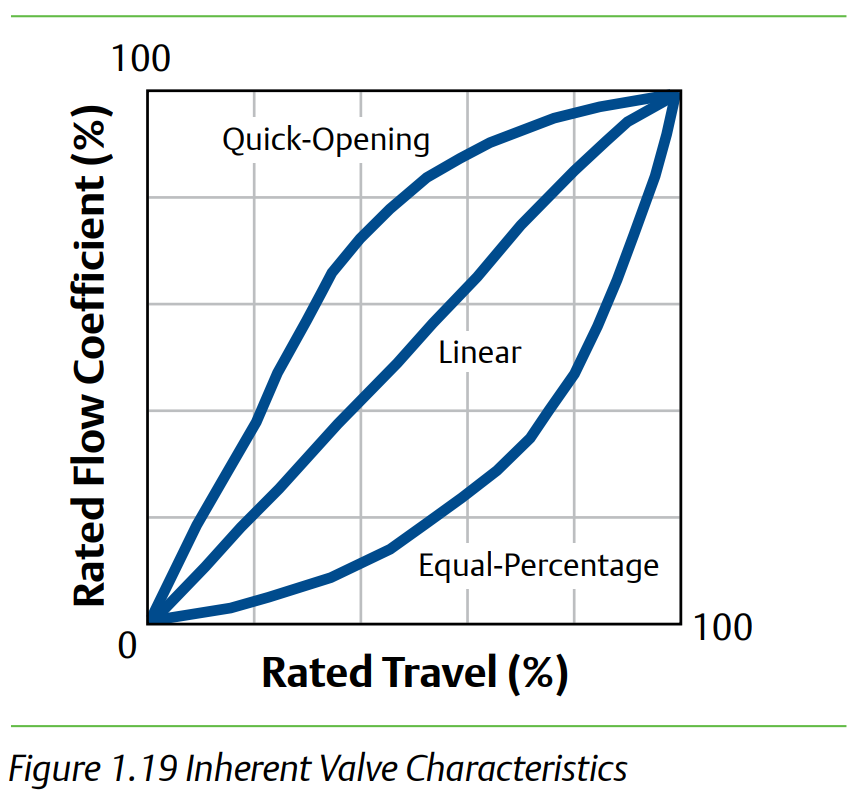
なお、フリーソフトと市販シミュレーターで紹介したSimCentralでは、GUI上でバルブ特性の編集が可能となっています。

以下のように、背景に特性線図のキャプチャを配置し、曲線がうまく一致するようにマウス操作でポイントを操作していくことで、ベンダー提供データ通りのバルブ特性を実装することができるようになっています。（ユーザーが指定したポイント間はSpline補間されます。）

非圧縮性流体のサイジング式

$$q= C \cdot A \sqrt{\frac{2 \Delta p}{\rho_1}}$$ $$C= \frac{C_d}{\sqrt{1-\beta^4}} $$

なお、ここで

\( \Delta p\)[kPa]：上下流の圧力損失

\( \beta\)[-]：絞り直径比(絞り直径/管直径)

\( \rho_1 \)[kg/m3]：入口密度

Reynolds数>2e5の領域では、C≒0.61

※Reynolds数は、入口径、入口物性より求めます。

圧縮性流体のサイジング式(ASME)

圧縮性流体の場合は、以下の膨張補正係数：Yを乗じます。

$$ Y = 1-(0.41 + 0.35 \beta^4) \cdot \frac{1-\Delta p}{\kappa} $$

なお、ここで

\( \kappa \)[-]：アイゼントロピック指数

なお、JISでは膨張補正係数として以下の式が用いられます。（JIS Z 8762-2:2007 (1)式）

$$ Y = 1-(0.351 + 0.256 \beta^4 + 0.93 \beta^8) \cdot \left[1 - \left( \frac{p_2}{p_1} \right)^{1/ \kappa} \right]$$

ISO 5167-1, 2：5167-1のTable A.1参照

出展

主に以下CraneのFlow of Fluidsを参考にしています

Crane Valve ; "Flow of Fluids Through Valves, Fittings & Pipe"

参考までに以下AVEVA社のSimCentralでの計算例をご紹介します。

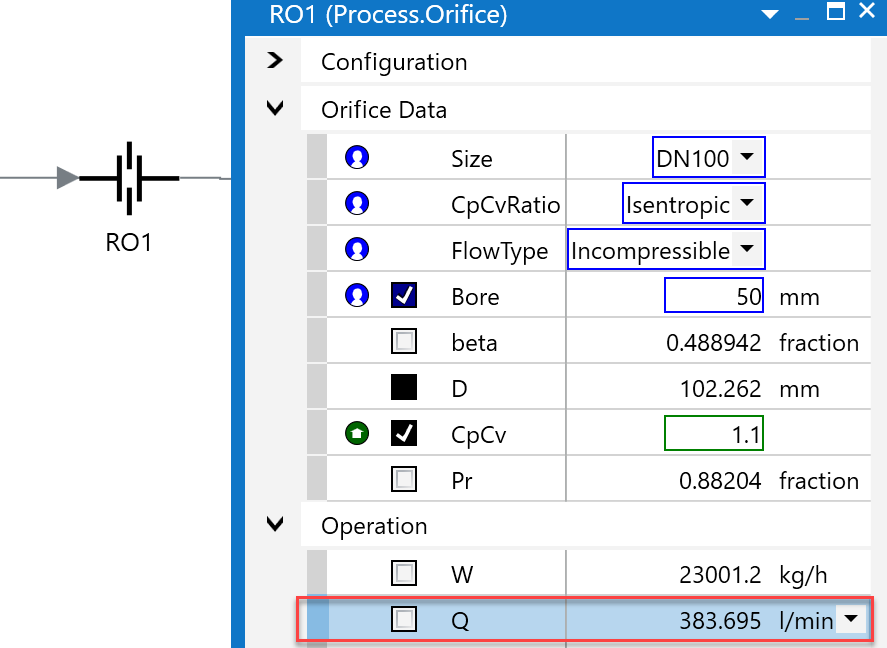
上述のCrane 2011年版、Example 7-23に液サービスでのオリフィス流量計算例が載っていますので、同様の計算をSimCentralで計算してみます。

計算条件：100mm Sch40の鋼管に、50mm径のSquare edgedオリフィスを挿入します。流体は15Cの水で、水銀圧力計は110mmを指しているものとします。流量係数Cと流量を求める例が示されており、結果として流量は383[l/min]となっていますが、以下SimCentralでも同様の結果が得られていることが確認できます。

SimCentralを用いる場合、さらにこの状態で非定常モードに移行することも可能です。

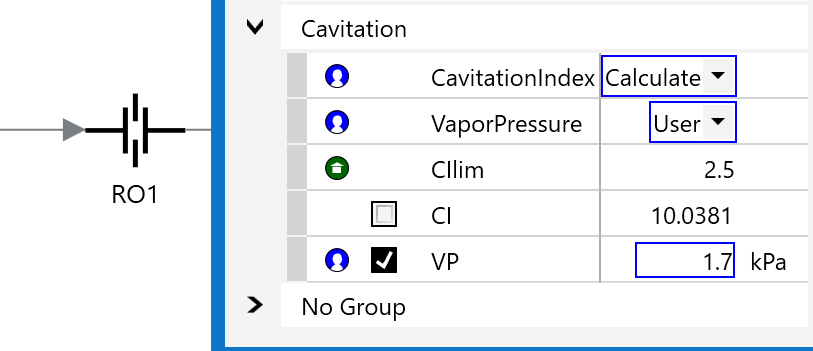
バルブのキャビテーション指標として、一般的に以下のキャビテーションインデックス：\( \sigma \)が用いられます。

$$ \sigma = \frac{P_2 - P_v}{P_1 - P_2}$$

なお、ここで

\( P_1\)[kPa]：バルブより1×直径分上流の圧力

\( P_2\)[kPa]：バルブより5×直径分上流の圧力

\( P_v\)[kPa]：入口温度における蒸気圧力

\( \sigma \)が大きいほどキャビテーションの影響は小さくなります。

以下出展記載のハンドブックにはグローブバルブ、バタフライ弁、ボール弁の参考\( \sigma \)値が記載されています。（キャビテーションが始まるIncipient\( sigma\)、完全にキャビテーションが発生していると考えられるChoked\( sigma\)の代表的な値が記載されていますのでご参照ください。）

出展

主に以下Valve Handbookを参考にしていますが、こちらのページも参考になります。

Philip L. Skousen ; "Valve Handbook"

AVEVA社のSimCentralでは、キャビテーションインデックスの計算機能が搭載されており、キャビテーションインデックスが指定した値を下回った場合にワーニングを出す機能がついています。(蒸気圧の自動推算機能も搭載されています)

実験結果とシミュレーション結果の比較がまとまっている論文として、以下Contractorの論文が参考になります。

出展

以下の論文が参考になります。

Contractor, D.N. "The Reflection of Waterhammer Pressure Waves from Minor Losses." 08 August 1964. Journal of Basic Engineering, Vol 87.

AVEVA社のSimCentralでは、水撃計算の専用ライブラリが搭載されており、以下のように簡単に水撃計算を行うことが可能です。

API RP 520参照

$$F=\frac{44.75159 \cdot Position \cdot Area \cdot K_d \cdot F_2 \cdot \sqrt{DP \cdot R \cdot MW}}{MW}$$

ただし、液の場合\(F_2\)は1、ガスの場合は以下式より求めます

$$F_2=\sqrt{\left(\frac{C_p/C_v}{C_p/C_v-1}\right) \cdot \left(\frac{P_x}{P_i}\right)^{2C_v/C_p} \cdot \left(\frac{1-\left(\frac{P_x}{P_i}\right)^{\frac{C_p/C_v-1}{C_p/C_v}}}{1-\frac{P_x}{P_i}}\right)}$$

F:モル流量、Kd：Discharge Coefficient、Cp/Cv：比熱比、R：モル密度、Pi：入口圧力、Px：出口圧力

$$F=\frac{0.02119 \cdot Position \cdot C \cdot Area \cdot K_d \cdot \sqrt{DP \cdot UGC \cdot R \cdot MW}}{MW}$$

ただし、Cは以下式より求めます

$$C=520 \cdot \sqrt{C_p/C_v \cdot \left(\frac{2}{C_p/C_v+1}\right) \cdot \left(\frac{C_p/C_v+1}{C_p/C_v-1}\right)}$$

必要面積の算出

ASME Codeで規定されている必要面積は以下の式より求めます。

$$ A=\frac{277.8W}{K_d K_b K_c K_v G}$$

各パラメーターは以下の通り。

Kd : discharge coefficient/p>

ガスサービスの場合は、0.975。

液サービスの場合は、subcooled：0.85, 飽和液：0.65を使用。

Kb : backpressure correction factor ()

KbはAPI記載のチャートより求めます。

Kc : combination crrection factor

PRVの上流にrapture diskが有る場合：0.9、無い場合：1.0。

Kv : viscosity correction factor

API記載のチャートから求めるか、以下の式により算出。

$$K_v=\left(0.9935+\frac{2.878}{Re^{0.5}}+\frac{342.75}{Re^{1.5}}\right)^{-1.9}$$ ２相流▼

層流域の摩擦係数式（Hagen-Poiseuille lawからの導出）

$$f=\frac{64}{Re}$$

平滑管の摩擦係数式

適用範囲：Re>4000

$$\frac{1}{\sqrt{f}}=2log_{10}(Re\sqrt{f})-0.8$$

遷移域の摩擦係数式（Colebrook-White式）

$$\frac{1}{\sqrt{f}}=1.14-2log_{10}(\epsilon/D+9.35/Re\sqrt{f})$$

乱流域の摩擦係数式（Colebrook式）

Colebrook式適用範囲：Re>4000

$$\frac{1}{ \sqrt {f} }=-2log\left(\frac{\epsilon/D}{3.7}+\frac{2.51}{Re\sqrt{f}}\right)$$

Colebrook式は収束計算が必要となりますので、計算例として、ExcelのGoalSeakを用いる方法、VBAを用いた計算方法をご紹介します。

なお、本サイトでは以下Darcy式を圧損計算の基本式として使っています。

$$DP=f \cdot \frac{L}{D} \frac{v^2}{2g}$$

機械系ではFanningの式を用いる場合が多いかもしれませんが、その場合は、前述の摩擦係数は1/4になります。

計算しやすいように、以下のような単純な数値で圧損計算を行っていきます。

流量W：100[t/hr]、配管径D：1.0[m]、配管長L：100[m]、配管粗さε：0.05[mm]

密度ρ：1[kg/m3]、粘度μ：1[cP]、フィッティング無し。

流速を計算します。

$$V=\frac{W}{\rho} \cdot \frac{1}{D^2/4 \cdot \pi}=\frac{100000[kg/hr]}{1[kg/m3]} \cdot \frac{1}{1^2/4 \cdot \pi [m^2]}=127324[m/hr]$$

続いてReynolds数を求めます。

$$Re=\frac{V \cdot \rho \cdot D}{\mu}=\frac{127324/3600[m/s] \cdot 1[kg/m3] \cdot 1[m]}{1/1000[Pa \cdot s]}=35368[-]$$

摩擦係数fは、Colebrook式で求める場合、上述のように収束計算が必要となります。

まずはGoalSeekで求める方法です。以下のように、適当なｆを初期値として与え、Colebrook式の左辺、右辺の計算を行い、左辺と右辺の差が0となるようにGoalSeekで設定します。

GoalSeekだとエラー値の評価が甘いですが、Solverを使えば、Error値を小さくすることができます。

VBAで求める場合は、例えば逐次代入法を用いて解くことができます。（Do Loopで、右辺の値の２乗の逆数を更新していき、前回値との差分がtolerance以下になるまで計算を繰り返します。）

以下のように関数として登録しておき、ExcelからVBA関数を呼び出すことが可能です。

また、MillerのFlow Measurement(Flow Measurement Engineering Handbook 3rd (third) Edition by Miller Richard published by McGraw-Hill Professional (1996))ではNewton法による解法が紹介されています。

具体的には、以下のように陽関数の形に変換し、微分値を求め、初期値f0から計算を行います。

$$F= - f^{-1/2} -2log\left(\frac{\epsilon/D}{3.7}+\frac{2.51}{Re\sqrt{f}}\right)$$ $$F'= \frac{1}{2} f^{-3/2} -\frac{4.034}{(\epsilon/D)Ref^{3/2}+9.287f}$$ $$f0= 0.25 \left[log \left( \frac{0.2703 \epsilon}{D} + \frac{5.74}{Re^{0.9}} \right) \right]^{-2} $$

諸条件から圧損を求める簡易ツールをこちらに作成しました。簡易版ですが、確認用にご使用ください。(※こちらのツールはSilverlightで作成しています。Internet Explorerでご利用ください。)

Crane記載式を以下ご紹介します。

$$ v_s = \sqrt{\gamma RT} $$

ここで、\(\gamma\)は比熱比になります。

超音速の判定は通常配管出口で行います。（DYNSIMでは出口で判定するか、もしくは全ての分割セクションで行うかの選択が可能です。配管内で絞り等が無い限りは出口判定で問題ありません。）

エルボーやティー等、フィッテイングの圧損を考える場合、前述のDP計算において\(K=f \cdot L/D\)に以下の補正をかけます。

$$K=f \cdot \frac{L}{D}$$

各フィッティングのK値については、以下代表的なものを記載いたします※Crane Engineering Handbook "K" Factor Tableより一部抜粋。

Fitting K value	K
Gate valves (Wedge Disc)	8f
Swing Check valves	100f
Stop Check valves	400f
Glove valves	340f
Ball valves	3f
Butterfly valves (2 to 8")	45f
Butterfly valves (10 to 14")	35f
Butterfly valves (16 to 24")	25f
Standard elbows (90°)	30f
Standard elbows (45°)	16f
Standard tees (Flow through branch)	60f
Standard tees (Flow through run tees)	20f
Pipe Engrance(Inward Projecting)	0.78
Pipe Exit	1.0

ザックリ相当長ベースで入力したい場合は、以下式にて相当長\(L_{eq}\)を入力します。

$$K=f \cdot \frac{L+L_eq}{D}$$

急拡大、急縮小による損失

急拡大、急縮小等、K値の補正が必要な場合は、以下式を使用します。（徐々に管径が変わる場合は、こちらをご参照ください）

$$K=f \cdot \frac{L+L_eq}{D} + K_{additional}$$

急拡大

$$K_{additional}=\left(1-\frac{d_{1}^2}{d_{2}^2}\right)^2$$

急縮小

$$K_{additional}=0.5\left(1-\frac{d_{1}^2}{d_{2}^2}\right)$$

※1,2の添え字はそれぞれ小口径、大口径配管を示しています。

代表的なフローパターンをいくつかご紹介します。

Bakerチャート

簡単に求められるフローパターンマップとして、Bakerチャートをご紹介します。

Bakerチャートの作り方

以下は、２相流の水平配管に対し、AVEVA Process Simulationで求めた各種運転条件から現在Bakerチャート上のどこに運転点があるかを求めた例になります。（作図はC#のoxyplotで行っています）

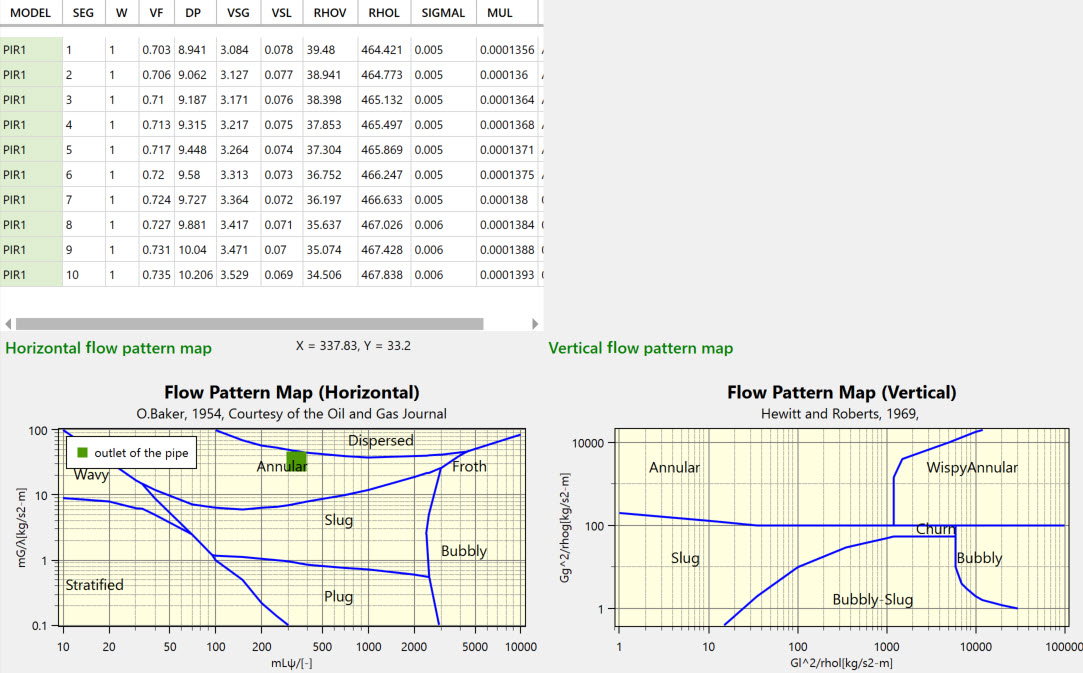
Bakerチャートは各相の流速、密度、粘度、表面張力が分かっていれば、簡単に求めることができます。

Bakerチャートの注意点

参考

Perry's Chemical Engineers' Handbook, Eighth Edition

Taitel-Duklerチャート

2相流配管の圧損計算式としてBeggs-Brill式を紹介します。

出典

Beggs, H.D. and Brill, J.P.; "A study of two-phase flow in inclined pipe;" Journal of Petroleum Technology, 1973, p.607–617

Beggs-Brill式の精度について

Baker, A., Nielsen, K., and Gabb, A; "Pressure loss, liquid-holdup calculations developed" Oil and Gas Journal, 1988, p.55–59

DYNSIMやSimCentralではBeggs-Brill式の選択が可能です。

2相流配管の圧損計算式としてLockhart-Martineli式を紹介します。

Lockhart-Martineli式の基本的な考え方

考え方はBBMHよりも単純で気相、液相が単相で流れた場合の圧損比をLockhart-MartineliのパラメーターXの相関式で表現し、以下のように計算します。

１．液側、ガス側のReynolds数を求める。⇒各相がTurbulentかLaminarか判断する。⇒使用する係数式が決まる

２．液側の圧力損失を計算する。（液側の重量流量、密度からColebrook式等で通常通り計算する）

３．１で求めた係数と２で求めた液側の圧力損失を掛け合わせて、２相流の圧力損失を求める。

Lockhart-Martineli式の精度について

Perryのhandbookに以下の記載があります。

1. 1inchもしくは、それ以下の場合、±50パーセントの精度。

2. フローパターンがStratified, wavy, slug flowsの場合は精度が高いが、annular flowの場合は精度が低い。

3. 4inch程度までは同等の精度が期待できる。

参考

Perry's Chemical Engineers' Handbook, Eighth Edition

簡単のため、まずは水のみ、密度一定とした場合の偏流計算を考えてみます。

下図のように、圧力P1のタンクから、各ユーザー（User1、User2）に、流れる流量を考えます。

上図で、送出元と各ユーザーの到達圧、密度が分かっている場合、配管径が決まれば、ヘッダー圧、各ユーザーへの流量は簡単に求めることができます。

例えば、以下のような問題設定で考えてみます。

まず未知数を見てみます。赤字で示していますが、各配管での流量、圧損とヘッダー圧の計７変数が未知数の状態ですので、７つの式が必要となります。

今回は密度一定、つまり非圧縮性の流体を考えていますので、物質収支、圧力バランスで蓄積項を考慮する必要は無く、以下のように考えられます。今回はNewton法で求めるため、予めf(x)=0の形に変形しておきます。

これで７変数に対し、７つの式を立てることができ、自由度は満足していますので、後は解くだけです。

とはいえ、流量-圧損の関係式が非線形となっており、式を見てパッと解ける連立方程式にはなっていないため、今回は①Pythonを使ってNewton-Raphson法で解く方法と、②Excelのsolverを使う方法をご紹介します。

Pythonで求める場合

まずは境界条件と適当な初期値を決めます。初期値は適当ですが、一応マスバランスは満たした形で決めておきます。

f(x)=の誤差がtolerance内に収まるまで繰り返し計算を行います。ここで、逆流が発生した場合に、ルート内が負とならないように場合分けしておきます。

あとはJacobianを手計算で求め、その逆行列と関数をかけ合わせれば良いのですが、ここでnumpyでは非常に便利な関数があります。

linalg.solve(Jacobian、関数)で、Jacobianと関数の積を一気に求めることができます。

刻み0.5、tolerance：e-5で、収束回数：14回。最終的な解は以下のように求まります。

なお、前述のように、逆流が発生する場合の式処理も行っておけば、以下のようにユーザー側の圧力が上昇した場合の逆流も計算することが可能です。

なお、以下のように収束計算の初めに摩擦係数を計算させてしまえば（収束計算になります）、配管径、配管長、フィッティング情報からconductance値を求めることも可能です。

Cf)Csharpで求める場合

上述のPythonを使ったケース同様、逆行列計算さえできれば簡単に解くことができます。

C++では、数値計算ライブラリとしてEigenが有名ですが、Csharpでも同様のものを探していたところ、Math.Net.Numericsというものがありました。

詳細は、Csharpのページでゆくゆくまとめていきたいと思いますが、ひとまず暫定版として、上述のPythonと同様の簡易サンプルを以下に作成しました。

Newton法による簡易偏流計算

簡単な使い方を以下に記載します。

Cf)シミュレーターで求める場合

上述のような偏流計算はシミュレーターであれば簡単に求めることが可能です。

例として、AVEVA社のプロセスシミュレーターSimCentral®を使用した例をご紹介します。

上記シミュレーターの詳細についてはフリーソフトと市販シミュレーターをご参照ください。

C#の例では、密度を一定としていましたが、シミュレーターでは厳密な物性を使用して計算できます。また、配管を複数セグメントに分割したり、外部環境（大気、土壌中等）との伝熱を考慮することも可能です。

参考ファイルはこちらをご参照ください。

また、SimCentralの場合は、水撃計算も行うことが可能です。

Excelで求める場合

Excelを使う場合、いくつか方法が考えられます。①VBAを使って上述のようにNewton-Raphson法を用いる方法、②Excelのシート上でNewton-Raphson法を用いる方法（Excelであれば逆行列計算、行列積も関数で行うことができます。）、③①と②の複合（②だけで行うと収束計算分セルを拡張する必要があるので、VBAと複合して使った方が見やすい結果になります）、④Solverを使う方法等です。

①～③はPythonを使う方法と考え方は同様なので省略し、④の方法を紹介します。

問題設定はPythonの場合と同様とします。

$$DP= K \cdot \rho \cdot \frac{v^2}{2} $$

※DP[Pa]

拡大管の場合

$$　\cdot \theta \leq 45 $$ $$　\ K = 2.6 * sin ( \frac{\theta}{2} ) * ( 1- \beta^2 )^2$$ $$　\cdot \theta >45 $$ $$　\ K = ( 1- \beta^2)^2$$

縮小管の場合

$$　\cdot \theta \leq 45 $$ $$　\ K = 0.8* sin ( \frac{\theta}{2} ) * ( 1- \beta^2) $$ $$　\cdot \theta >45 $$ $$　\ K = 0.5 * \sqrt{sin ( \frac{\theta}{2} ) } * ( 1- \beta^2) $$

拡大管/縮小管の圧損計算式の出典

・Crane Valve ; "Flow of Fluids Through Valves, Fittings & Pipe"

簡易の計算ツールを作成しましたので、こちらのリンクから計算可能です

トレイ塔の渇き圧損の推算法について、トレイタイプ毎に代表的な推算式を記載します。

　 Sieveトレイ（Fair式）

$$ \Delta P = \frac{0.186}{C_v^2} \frac{ \rho_v }{\rho_l} U_v^2$$

出典

The correlation of Fair, J. R., “How to Predict Sieve Tray Entrainment and Flooding”

ここで、\( C_v \)：Discharge coefficientは、Tray thickness/Hole Diameterと、Hole area/Active Areaより、以下のチャートより求めます。

出典

Leibson, I., R.E.Kelley, and L.A.Bullington, Pet. Ref., 36(2),p.127, 1957

　 Bubble Capトレイ

$$ \Delta P = 1.2 \frac{ \rho_v }{\rho_l - \rho_v }^{0.2} U_v^{0.4}+ K_2 \frac{ \rho_v }{\rho_l} U_v^2$$

出典

Bolles, W.L., “Optimum Bubble Cap Tray. Design,”

Applied Process Design for Chemical and Petrochemical Plants, Vol.2, 第３版に記載されている例題8-36を検算してみます。

計算前提

カラムの設定条件：

トレイ塔の水塔圧損の推算法について、トレイタイプ毎に代表的な推算式を記載します。

　 Sieveトレイ

充填塔の渇き圧損計算式としてSticlmair式をご紹介します。

粒子径の相当長[m]:\(Dia_P\)は、ベッドのVoid fraction、充填物の比表面積[1/m]：PackAreaを用いて下式となります。

$$Dia_P=\frac{6 \cdot \left(1-Void\right)}{PackArea}$$

充填塔の空塔速度[m/sec]:\(U_v\)は、ガスの通過流量[kg-mol/sec]:\left(F_v\rght)と、ガス密度[kg-mol/m3]:\(R_v\)、カラムの断面積[m2]:Aを用いて下式となります。

$$U_v=\frac{F_v}{R_v A}$$

抵抗係数[-]:\(f_0\)は、Stichlmair係数[-]：C1～C3とガスのレイノルズ数[-]:\(Re_{vap})を用いて下式となります。

$$f_0=\frac{C_1}{Re_{vap}}+\frac{C_2}{2 \cdot \sqrt{Re_{vap}}}+C_3$$ $$c=\frac{\left(- \frac{C_1}{Re_{vap}} - \frac{C_2}{2 \cdot \sqrt{Re_{vap}}}\right)}{f_0}$$ $$\Delta P_d = \frac{1}{1000 \cdot KJ^2}\frac{3}{4}f_0 \frac{1-Void}{Void^{4.65}}R_{gas} \frac{PackHeight}{Dia_P}U_v^2$$

最終的な渇き圧損[kPa]:\( \Delta P\)は、下式となります。

$$\Delta P = \Delta P_d \left(\frac{1-Void \cdot \left(1-\frac{Beta}{Void}\right)}{1-Void}^{\frac{2+c}{3}}\right) \cdot \left(1-\frac{Beta}{Void}\right)^{-4.65}$$

Stichlmair係数C1～C3、比表面積、Void Fractionは各充填物タイプに応じて求められています。

以下に一部抜粋して示します。詳細は出展をご参照ください。

規則充填物

Packing	Type/size	area[1/m]	void[-]	C1[-]	C2[-]	C3[-]
MontZ	B1/300	300	0.97	2	3	0.9
	B1/200	200	0.98	2	4	1.0
	B1/100	100	0.99	2	7	1.0
Sulzer	Mellapak(plastic)/250Y	250	0.85	1	1	0.32

出典

Stichlmair, J.J., Bravo, J.L., Fair, J.R.,; “General model for prediction of pressure drop and capacity of counter current gas/liquid Packed Columns” Gas Separation & Purification,. Vol. 3, March 1989, p. 19-28

充填塔のフラッディング計算

Stichlmairの式 　　

充填塔の渇き圧損計算式としてSticlmair式をご紹介します。

　　

以下の流れで収束計算を行います。

　　

a.ガス流速を仮定します。

　　

b.乾き圧損を計算します。

　　

c.濡れ圧損を計算します。

　　

d.下式の残差を求め、収束誤差を超えている場合は再度ガス流速をアップデートし、aに戻ります。

こちらのリンクから計算可能です

出典

Stichlmair, J.J., Bravo, J.L., Fair, J.R.,; “General model for prediction of pressure drop and capacity of counter current gas/liquid Packed Columns” Gas Separation & Purification,. Vol. 3, March 1989, p. 19-28

トレイ塔のフラッディング計算法として、以下の書籍による２つの計算法をご紹介します。

出典1

Glitsch Ballast Tray Design Manual Bulletin 4900

出典2

Kister, H. Z. “Distillation Design”, McGraw-Hill Book Company Page.279

上記の両書とも、以下のSouders-Brown係数を用いて計算されます。

Souders-Brownの係数

$$\sqrt{\frac{\rho_{vap}}{\rho_{liq}-\rho_{vap}}}$$ Glitsch法 Kister and Haas correlationを使った推算法

推奨適用範囲として圧力範囲やガス流速、液ロード、密度等記載されているので、使用する際には適用範囲を確認したほうが良いかと思います。（出展２のPage.282）

またトレイタイプとしては、SieveもしくはValveとされています。

Weeping量の推算式としてPerryのエンジニアリングハンドブックには以下Lockett and Banick correlationsが紹介されています。（DYNSIMでも同様の式が使用可能です）

トレイ穴径におけるFroude数\(Fr_h\)に応じて式の使い分けがなされていますが、以下Froude数0.2以上で用いられる式をご紹介します。

$$ \frac{W}{A_h} = \frac{1.841}{Fr_h^1.533} $$